题目内容
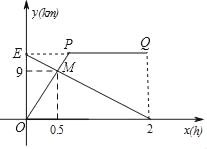
【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x(h)之间的函数关系,且OP与EF相交于点M.
(1)求线段OP对应的y甲与x的函数关系式(不必注明自变量x的取值范围);
(2)求y乙与x的函数关系式以及A,B两地之间的距离;
(3)请从A,B两题中任选一题作答,我选择 题.
A.直接写出经过多少小时,甲、乙两人相距3km;
B.设甲、乙两人的距离为s(km),直接写出s与x的函数关系式,并注明x的取值范围.
【答案】(1)线段OP对应的函数解析式为y甲=18x;(2)A、B两地的距离是12km;(3)见解析.
【解析】
(1)根据函数图象中的数据可以求得相应的函数解析式;
(2)根据图象中的数据可以求得相应的函数解析式和AB两地的距离;
(3)任选一题,然后根据(1)和(2)中的函数解析式即可解答本题.
解:(1)设线段OP对应的函数解析式为y甲=kx,
9=0.5k,得k=18,
∴线段OP对应的函数解析式为y甲=18x;
(2)设y乙与x的函数关系式是y乙=mx+n,
![]() ,得
,得![]() ,
,
即y乙与x的函数关系式是y乙=﹣6x+12,
当x=0时,y乙=12,
∴A、B两地的距离是12km;
(3)请从A,B两题中任选一题作答,我选择B题,
故答案为:B,
B题:当0≤x≤0.5时,s=(﹣6x+12)﹣18x=﹣24x+12,
甲到达B地用的时间为:12÷(9÷0.5)=![]() 小时,
小时,
当0.5<x≤![]() 时,s=18x﹣(﹣6x+12)=24x﹣12,
时,s=18x﹣(﹣6x+12)=24x﹣12,
当![]() <x≤2时,s=12﹣(﹣6x+12)=6x.
<x≤2时,s=12﹣(﹣6x+12)=6x.
补充:若选A,解答如下,
当0≤x≤0.5时,(﹣6x+12)﹣18x=3,解得,x=![]() ,
,
当0.5<x≤![]() 时,18x﹣(﹣6x+12)=3,得x=
时,18x﹣(﹣6x+12)=3,得x=![]() .
.

 阅读快车系列答案
阅读快车系列答案