Question

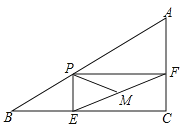
【题目】在Rt△ABC中，∠C=90°，AB=5，AC=3，点P为边AB上一动点（且点P不与点A，B重合），PE⊥BC于E，PF⊥AC于F，点M为EF中点，则PM的最小值为（　　）

A.B.C.D.

Answer 1

【答案】D

【解析】

首先证明四边形CEPF是矩形，因为M是EF的中点，推出延长PM经过点C，推出EF=CP，可得PM=EF=PC，求出PC的最小值可得PM的最小值．

解：在Rt△ABC中，∵∠ACB=90°，AB=5，AC=3，

∴BC==4，

∵PE⊥BC于E，PF⊥AC于F，

∴∠PEC=∠PFC=∠EPF=90°，

∴四边形CEPF是矩形，

∵M是EF的中点，

∴延长PM经过点C，

∴EF=CP，PM=EF=PC，

当PC⊥AB时，PC=，

∴PM的最小值为，

故选：D．