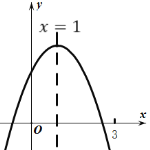题目内容
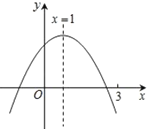
【题目】二次函数![]() (
(![]() )的图象如图所示,下列结论:①
)的图象如图所示,下列结论:①![]() ;②
;②![]() ;③
;③![]() 为任意实数,则
为任意实数,则![]() ;④
;④![]() ;⑤
;⑤![]() ,其中正确的有( )
,其中正确的有( )
A.①②③B.②④C.②⑤D.②③⑤
【答案】C
【解析】
根据抛物线开口方向得a<0,由抛物线对称轴为直线x=-![]() =1,得到b=-2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;当x=3时函数值小于0,y=9a+3b+c<0,且x=-
=1,得到b=-2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;当x=3时函数值小于0,y=9a+3b+c<0,且x=-![]() =1,即b=-2a,从而求得
=1,即b=-2a,从而求得![]() .
.
∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=-![]() =1,
=1,
∴b=-2a>0,即2a+b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线对称轴为直线x=1,
∴函数的最大值为a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③错误;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(-1,0)的右侧
∴当x=-1时,y<0,
∴a-b+c<0,所以④错误;
当x=3时函数值小于0,y=9a+3b+c<0,且x=-![]() =1,
=1,
即b=-2a,代入得9a+6a+c<0,得![]() ,所以⑤正确.
,所以⑤正确.
综上所述,正确的有②⑤.
故选C.

 名校课堂系列答案
名校课堂系列答案【题目】某班数学兴趣小组经过市场调查,整理出某种商品在第![]() 天的售价与销量的相关信息如下表:
天的售价与销量的相关信息如下表:
观察表格:根据表格解答下列问题:
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
(1)![]() __________.
__________.![]() _____________.
_____________.![]() ___________.
___________.
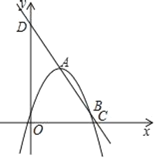
(2)在下图的直角坐标系中画出函数![]() 的图象,并根据图象,直接写出当
的图象,并根据图象,直接写出当![]() 取什么实数时,不等式
取什么实数时,不等式![]() 成立;
成立;
(3)该图象与![]() 轴两交点从左到右依次分别为
轴两交点从左到右依次分别为![]() 、
、![]() ,与
,与![]() 轴交点为
轴交点为![]() ,求过这三个点的外接圆的半径.
,求过这三个点的外接圆的半径.