题目内容
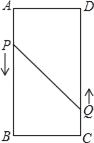
【题目】如图所示,矩形![]() 中,
中,![]() 厘米,
厘米,![]() 厘米(
厘米(![]() ).动点
).动点![]() 同时从
同时从![]() 点出发,分别沿
点出发,分别沿![]() ,
,![]() 运动,速度是
运动,速度是![]() 厘米/秒.过
厘米/秒.过![]() 作直线垂直于
作直线垂直于![]() ,分别交
,分别交![]() ,
,![]() 于
于![]() .当点
.当点![]() 到达终点
到达终点![]() 时,点
时,点![]() 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为![]() 秒.
秒.
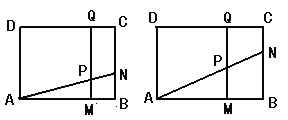
(1)若![]() 厘米,
厘米,![]() 秒,求PM的长度;
秒,求PM的长度;
(2)若![]() 厘米,求出某个时间
厘米,求出某个时间![]() ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求![]() 的取值范围;
的取值范围;
【答案】(1)![]() (2)
(2)![]() ,使
,使![]() ,相似比为
,相似比为![]()
(3)![]() ,
,
【解析】
(1)容易知道△ANB∽△APM,利用相似三角形的对应边成比例就可以求出PM;
(2)若PNB∽△PAD,则![]() ,而
,而![]() ,∴
,∴![]() ,则可求出t,也可以求出相似比;
,则可求出t,也可以求出相似比;
(3)首先用△AMP∽△ABN把QM,PM用t表示,再用t表示梯形PMBN与梯形PQDA的面积,根据已知可以得到关于t的方程,再由t与a的关系式可以求t的取值范围了;
(4)由(3)根据梯形PQCN的面积与梯形PMBN的面积相等得到关于t的方程,求出t,再求出a,则问题可解.
解:(1)当t=1时,MB=1,NB=1,AM=4-1=3,
∵PM∥BN
∴△ANB∽△APM,
∴![]() ,
,
∴PM=![]()
(2)当t=2时,使△PNB∽△PAD,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]()
解得t=2,则相似比为2:3.
(3)![]() ,
,
⊿APM∽⊿ABN ,
![]() ,
,
即:![]()
∴![]()
当梯形![]() 与梯形
与梯形![]() 的面积相等,即
的面积相等,即![]()
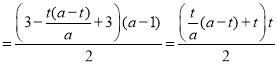
化简得![]() ,
,
![]() ,
,
![]() ,
,
则![]() ,
,

 阅读快车系列答案
阅读快车系列答案【题目】某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如表:
原科维生素C及价格 | 甲种原料 | 乙种原料 |
维生素c(单位/千克) | 600 | 400 |
原料价格(元/千克) | 9 | 5 |
现要配制这种营养食品20千克,设购买甲种原料x千克,购买这两种原料的总费用为y元.
(1)求y与x的函数关系式?
(2)若食堂要求营养食品每千克至少含有480单位的维生素C,试说明需要购买甲种原料多少千克时,总费用最少?最少费用是多少元?