题目内容
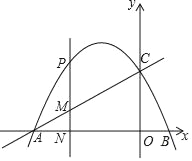
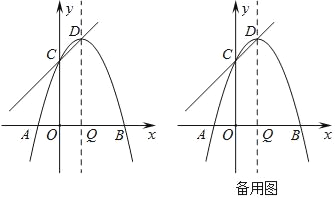
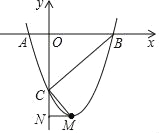
【题目】二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣
,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣![]() 或﹣
或﹣![]() .其中正确的有_____.(请将正确结论的序号全部填在横线上)
.其中正确的有_____.(请将正确结论的序号全部填在横线上)
【答案】①③④
【解析】试题解析:①∵![]()
∴抛物线开口向下,
∵图象与x轴的交点A、B的横坐标分别为-3,1,
∴当![]() 时,
时,![]() ,
,
即![]()
故①正确;
②∵图象与x轴的交点A、B的横坐标分别为-3,1,
∴抛物线的对称轴是:![]()
![]()
![]()
由对称性得:![]() 与
与![]() 是对称点,
是对称点,
∴则![]()
故②不正确;
③∵![]()
∴![]()
当x=1时,y=0,即![]()
![]()
![]() ,故③正确;
,故③正确;
④要使![]() 为等腰三角形,则必须保证
为等腰三角形,则必须保证![]() 或
或![]() 或
或![]()
当![]() 时,
时,
∵![]()
![]() 为直角三角形,
为直角三角形,
又∵OC的长即为|c|,
∴![]()
∵由抛物线与y轴的交点在y轴的正半轴上,
∴![]()
与![]() 联立组成解方程组,解得
联立组成解方程组,解得![]()
同理当![]() 时,
时,
∵![]() 为直角三角形,
为直角三角形,
又∵OC的长即为|c|,
∴![]()
∵由抛物线与y轴的交点在y轴的正半轴上,
∴![]()
与![]() 联立组成解方程组,解得
联立组成解方程组,解得![]()
同理当![]() 时,
时,
在![]() 中,
中,![]()
在![]() 中,
中,![]()
∵![]()
∴![]() ,此方程无实数解.
,此方程无实数解.
经解方程组可知有两个b值满足条件.
故④正确.
综上所述,正确的结论是①③④.
故答案为:①③④.

练习册系列答案
相关题目