题目内容
【题目】观察如图所示的图形,回答下列问题:
(1)按甲方式将桌子拼在一起.
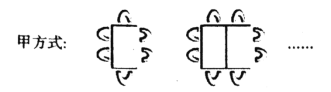
4张桌子拼在一起共有 个座位,n张桌子拼在一起共有 个座位;
(2)按乙方式将桌子拼在一起.
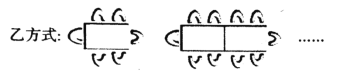
6张桌子拼在一起共有 个座位,m张桌子拼在一起共有 个座位;
(3)某食堂有A,B两个餐厅,现有102张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将a张桌子放在A餐厅,按甲方式每6张拼成1张大桌子;将其余桌子都放在B餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有404个座位,问A,B两个餐厅各有多少个座位?
【答案】(1)12,2n+4;(2)26,4m+2;(3)A餐厅有80个座位,B餐厅有324个座位.
【解析】
(1)观察图形发现,在一桌坐6个人基础上,每增加一张桌子多两个人,据此寻找规律求解即可;
(2)观察图形发现,在一桌坐6个人基础上,每增加一张桌子多四个人,据此寻找规律求解即可;
(3)根据(1)(2)中列出的关系式,分别求出每6张以及每4张时甲乙方式的座位数,再根据两个餐厅一共404个座位列出方程求解即可.
(1)观察可得,按该方式将4张桌子拼在一起共有12个座位,n张桌子拼在一起有![]() 个座位;
个座位;
(2)观察可得,按该方式将6张桌子拼在一起共有26个座位,m张桌子拼在一起有![]() 个座位;
个座位;
(3)按甲方式每6张桌子拼在一起能有座位:![]() 个;
个;
按乙方式每4张桌子拼在一起能有座位:![]() =18个;
=18个;
∴![]() ,
,
解得:![]() ,
,
∴A餐厅有30张桌子,共有80个座位,
B餐厅共有72张桌子,共有324个座位.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目