题目内容
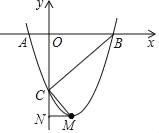
【题目】如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．
（1）求该抛物线所对应的二次函数的表达式及顶点M的坐标；
（2）连结CB、CM，过点M作MN⊥y轴于点N，求证：∠BCM=90°．
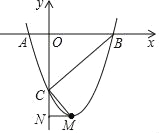
【答案】（1）y=x2﹣2x﹣3；M（1，﹣4）（2）90°
【解析】试题分析：（1）由抛物线与x轴交于点
两点，则可设抛物线解析式为
．由与y轴交于点
则代入易得解析式，顶点易知．
证明
，
为等腰直角三角形，即可求出
试题解析：（1）设该抛物线对应的二次函数的表达式为，
∵抛物线过点
∴3=a(0+1)(03)，
∴a=1，
∴抛物线解析式为
∵
∴M(1,4).
（2）
为等腰直角三角形，
轴于点N．
也是等腰直角三角形，
练习册系列答案
相关题目
