��Ŀ����
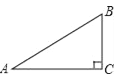
����Ŀ����ͼ��������y=��![]() x2+bx+c��ֱ��y=
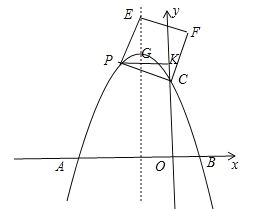
x2+bx+c��ֱ��y=![]() x+3��x�Ḻ�����ڵ�A����y���ڵ�C����x���������ڵ�B��
x+3��x�Ḻ�����ڵ�A����y���ڵ�C����x���������ڵ�B��
��1���������ߵĽ���ʽ��
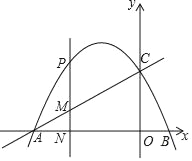
��2����PΪ������������һ�㣬���P�ĺ�����Ϊx��
������P�ڵڶ����ޣ�����P��PN��x����N����ֱ��AC�ڵ�M�����߶�PM����x�ĺ�������ʽ�������PM�����ֵ��
������P��������������һ�㣬����CP����CPΪ����������CPEF������E���������ߵĶԳ�����ʱ����ֱ��д����ʱ��P�����꣮
���𰸡���1�������߽���ʽΪy=��![]() x2��
x2��![]() x+3����2���ٵ�x=��2ʱ���߶�PM�ij������ֵ�����ֵΪ
x+3����2���ٵ�x=��2ʱ���߶�PM�ij������ֵ�����ֵΪ![]() ����P������Ϊ����4��0����
����P����������4��0����![]() ��
��![]() ����2��0����
����2��0����![]() ��
��![]() ����
����
�������������������1������һ�κ�������ʽȷ����C��0��3����A����4��0����Ȼ�����ô���ϵ����ȷ�������߽���ʽ��
��2������P��x����![]() x2��
x2��![]() x+3������4��x��0������M��x��
x+3������4��x��0������M��x��![]() x+3������PM=��
x+3������PM=��![]() x2��
x2��![]() x+3����
x+3����![]() x+3����Ȼ����ݶ��κ��������ʽ��������
x+3����Ȼ����ݶ��κ��������ʽ��������
����PK��y����K���������ߵĶԳ�����G����ͼ����֤����PEG�ա�CPK�õ�CK=PG����P��x����![]() x2��
x2��![]() x+3���������ߵĶԳ���Ϊֱ��x=��1����G����1����
x+3���������ߵĶԳ���Ϊֱ��x=��1����G����1����![]() x2��
x2��![]() x+3����K��0����
x+3����K��0����![]() x2��
x2��![]() x+3������PG=|��1��x|=|x+1|��CK=|��
x+3������PG=|��1��x|=|x+1|��CK=|��![]() x2��
x2��![]() x+3��3|=|��
x+3��3|=|��![]() x2��
x2��![]() x|������|x+1|=|��
x|������|x+1|=|��![]() x2��
x2��![]() x|��Ȼ������ֵ�������x���Ӷ��õ�����������P�����꣮
x|��Ȼ������ֵ�������x���Ӷ��õ�����������P�����꣮
���������������1����x=0ʱ��y=![]() x+3=3����C��0��3����
x+3=3����C��0��3����
��y=0ʱ��![]() x+3=0�������x=��4����A����4��0������A����4��0����C��0��3������y=��
x+3=0�������x=��4����A����4��0������A����4��0����C��0��3������y=��![]() x2+bx+c����
x2+bx+c����![]() �������
�������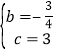 ���������߽���ʽΪy=��
���������߽���ʽΪy=��![]() x2��
x2��![]() x+3��
x+3��
��2������P��x����![]() x2��
x2��![]() x+3������4��x��0������M��x��
x+3������4��x��0������M��x��![]() x+3������PM=��
x+3������PM=��![]() x2��
x2��![]() x+3����
x+3����![]() x+3��=��
x+3��=��![]() x2��
x2��![]() x=��
x=��![]() ��x+2��2+
��x+2��2+![]()
��x=��2ʱ���߶�PM�ij������ֵ�����ֵΪ![]() ��
��
����PK��y����K���������ߵĶԳ�����G����ͼ�����ı���PEFCΪ����������PE=PC����EPC=90�㣮�ߡ�PGE=��PKC=90�㣬���PEG=��CPK���á�PEG�ա�CPK����CK=PG����P��x����![]() x2��
x2��![]() x+3���������ߵĶԳ���Ϊֱ��x=��1����G����1����
x+3���������ߵĶԳ���Ϊֱ��x=��1����G����1����![]() x2��
x2��![]() x+3����K��0����
x+3����K��0����![]() x2��
x2��![]() x+3������PG=|��1��x|=|x+1|��CK=|��
x+3������PG=|��1��x|=|x+1|��CK=|��![]() x2��
x2��![]() x+3��3|=|��
x+3��3|=|��![]() x2��
x2��![]() x|����|x+1|=|��
x|����|x+1|=|��![]() x2��
x2��![]() x|���ⷽ��x+1=��
x|���ⷽ��x+1=��![]() x2��
x2��![]() x����x1=��4��x2=��
x����x1=��4��x2=��![]() ��
��
�ⷽ��x+1=![]() x2+
x2+![]() x����x1=2��x2=��
x����x1=2��x2=��![]() ��
��
��P����������4��0����![]() ����2��0����
����2��0����![]() ����
����