题目内容
【题目】如图,AB=10cm,C是线段AB上一个动点,沿A→B→A以2cm/s的速度往返运动一次,D是线段BC的中点,设点C的运动时间为t秒(0≤t≤10).
![]()
(1)当t=2时,求线段CD的长.
(2)当t=6时,求线段AC的长.
(3)求运动过程中线段AC的长.(用含t的代数式表示)
(4)在运动过程中,设AC的中点为E,线段DE的长是否发生变化?若不变,直接写出DE的长;若发生变化,请说明理由.
【答案】(1)CD=3cm;(2)AC=8cm,(3)当0≤t≤5时,AC=2tcm,当5≤t≤10时,AC=(20﹣2t)cm;(4)线段DE的长不发生变化,DE=5cm.
【解析】
(1)根据AC=2t即可得出结论;
(2)当t=6时,去点C到达B后返回,根据AC=10-2t即可得出结论;
(3)分类讨论:当A→B即0≤t≤5时,当B→A即5≤t≤10时;
(3)直接根据中点公式即可得出结论.
(1)∵t=2,
∴AC=4cm,
∵AB=10cm,
∴CB=6cm,
∵D是线段BC的中点,
∴CD=3cm;
(2)∵t=6,
∴AC=10﹣2=8cm,
∵AB=10cm;
(3)当0≤t≤5时,AC=2tcm,
当5≤t≤10时,AC![]() ;
;
(4)DE=EC+CD=![]() AC+
AC+![]() CB=
CB=![]() (AC+CB)=
(AC+CB)=![]() AB=5cm,
AB=5cm,
∴线段DE的长不发生变化.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案【题目】一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把1,3,6,10,15,21,…,称为“三角形数”;把1,4,9,16,25,…,称为“正方形数”.
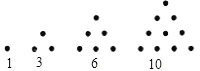

将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
五边形数 | 1 | 5 | 12 | 22 | C | 51 | 70 | … |
(1)按照规律,表格中a=___,b=___,c=___.
(2)观察表中规律,第n个“正方形数”是________;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是___________.