题目内容
【题目】一定数量的石子可以摆成如图所示的三角形和四边形，古希腊科学家把1,3,6,10,15,21，…，称为“三角形数”；把1,4,9,16,25，…，称为“正方形数”.
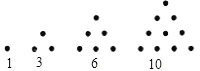
将三角形、正方形、五边形都整齐的由左到右填在所示表格里：
三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
五边形数 | 1 | 5 | 12 | 22 | C | 51 | 70 | … |
（1）按照规律，表格中a=___，b=___，c=___．
（2）观察表中规律，第n个“正方形数”是________；若第n个“三角形数”是x，则用含x、n的代数式表示第n个“五边形数”是___________．
【答案】 28 36 35 n2 n2 +x-n
【解析】分析：(1)、首先根据题意得出前6个“三角形数”分别是多少，从而得出a的值；前5个“正方形数”分别是多少，从而得出b的值；前4个“正方形数”分别是多少，从而得出c的值；(2)、根据前面得出的一般性得出答案．
详解：（1）∵前6个“三角形数”分别是：1=
、3=
、6=
、10=
、15=
、21=
，
∴第n个“三角形数”是
， ∴a=7×82=287×82=28．
∵前5个“正方形数”分别是： 1=12，4=22，9=32，16=42，25=52，
∴第n个“正方形数”是n2， ∴b=62=36．
∵前4个“正方形数”分别是：1=
，5=
，12=
，22=
，
∴第n个“五边形数”是n（3n1）2n（3n1）2， ∴c=
=35．
（2）第n个“正方形数”是n2；1+1-1=1，3+4-5=2，6+9-12=3，10+16-22=4，…，
∴第n个“五边形数”是n2+x-n．
【题目】如图，在矩形ABCD中，AB=6cm，AD=3cm，点P是边DC上一动点，设D，P两点之间的距离为xcm，P，A两点之间的距离为ycm.
小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小东的探究过程，请补充完整：
（1）确定自变量x的取值范围________；
（2）通过取点、画图、测量，得到了x与y的几组值，如下表：
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 3 | 3.1 | 3.6 | 4.3 |
| 5.8 | 6.7 |
（3）在下列网格中建立平面直角坐标系，描出补全后的表中各组数值对应的点，画出该函数的图象；
（4）结合画出的函数图象，解决问题：当PA=2AD 时，PD的长度约为______cm．
