题目内容
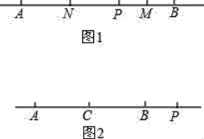
【题目】将一副直角三角板(![]() ,
,![]() )按图1方式摆放(即
)按图1方式摆放(即![]() 与
与![]() 重合、
重合、![]() 与
与![]() 共线).
共线).
(1)如图2,当![]() 绕点
绕点![]() 旋转至
旋转至![]() 时,求
时,求![]() 的度数:
的度数:
(2)若![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,回到起始位置停止,设旋转时间为t,当t为何值时,
的速度顺时针旋转,回到起始位置停止,设旋转时间为t,当t为何值时,![]() (
(![]() 与
与![]() 始终不共线);
始终不共线);
(3)若![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转的同时,
的速度顺时针旋转的同时,![]() 也绕点
也绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,当
的速度顺时针旋转,当![]() 回到起始位置时全都停止旋转.设旋转时间为t,在运动过程中,当t为何值时,
回到起始位置时全都停止旋转.设旋转时间为t,在运动过程中,当t为何值时,![]() 的边所在直线恰好平分
的边所在直线恰好平分![]() ?试直接写出t值.
?试直接写出t值.
【答案】(1)![]() ;(2)t=15秒或51秒;(3)t=3秒或9秒或15秒.
;(2)t=15秒或51秒;(3)t=3秒或9秒或15秒.
【解析】
(1)可证得![]() ,由
,由![]() 可求出
可求出![]() ,于是可解;
,于是可解;
(2)分两种情况讨论:![]() 在AC的右侧时;
在AC的右侧时;![]() 在AC的左侧时.分别画出图形,根据图形求出旋转的角度,即可求出时间t;
在AC的左侧时.分别画出图形,根据图形求出旋转的角度,即可求出时间t;
(3)时间的范围是是0≤t≤18.如果把![]() 看作是静止的,那么
看作是静止的,那么![]() 将绕点
将绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转.AB边在旋转过程中不可能平分
的速度顺时针旋转.AB边在旋转过程中不可能平分![]() ,所以可分四种情况讨论:
,所以可分四种情况讨论:
① AC边旋转至CP后平分![]() ;② AC边旋转至CP后,PC的延长线平分
;② AC边旋转至CP后,PC的延长线平分![]() ;③ BC边旋转至CP后平分
;③ BC边旋转至CP后平分![]() ;④BC边旋转至CP后,PC的延长线平分
;④BC边旋转至CP后,PC的延长线平分![]() .每种情况画出相应的图形,根据图形求出旋转的角度,即可求出时间t.
.每种情况画出相应的图形,根据图形求出旋转的角度,即可求出时间t.
解:(1)由题意可知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
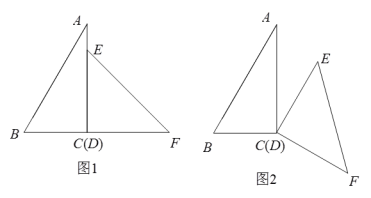
(2)分两种情况讨论:
如图3,作![]() ,
,
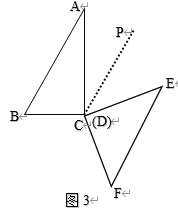
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (秒);
(秒);
如图4,![]() 与AB交于点G,
与AB交于点G,

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴旋转的角度=![]() ,
,
∴![]() (秒);
(秒);
综上所述,当t=15秒或51秒时,![]() ;
;
(3)∵当![]() 回到起始位置时全都停止旋转,
回到起始位置时全都停止旋转,
∴0≤t≤18,
∵![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转的同时,
的速度顺时针旋转的同时,![]() 也绕点
也绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,
的速度顺时针旋转,
∴如果把![]() 看作是静止的,那么
看作是静止的,那么![]() 将绕点
将绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,
的速度顺时针旋转,
AB边在旋转过程中不可能平分![]() ,下面分四种情况讨论:
,下面分四种情况讨论:
①如图5,AC边旋转至CP后平分![]() ,
,
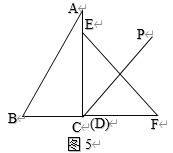
∴![]() ,
,
∴![]() (秒);
(秒);
②如图6,AC边旋转至CP后,PC的延长线平分![]() ,
,
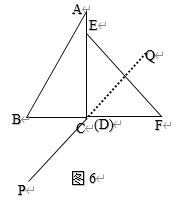
∴![]() ,
,
∴旋转的角度=![]() ,
,
∴![]() (秒);
(秒);
③如图7,BC边旋转至CP后平分![]() ,
,
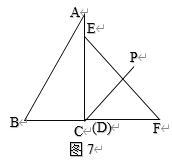
∴![]() ,
,
∴旋转的角度=![]() ,
,
∴![]() (秒);
(秒);
④如图8,BC边旋转至CP后,PC的延长线平分![]() ,
,

∴![]() ,
,
∴旋转的角度=![]() ,
,
∴![]() (秒)(不合题意,舍去);
(秒)(不合题意,舍去);
综上所述,当t=3秒或9秒或15秒时,![]() 的边所在直线恰好平分
的边所在直线恰好平分![]() .
.

【题目】“五一”期间,文具店老板购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 14 |
B型 | 15 | 22 |
(1)老板如何进货,能使进货款恰好为1350元?
(2)要使销售文具所获利润不少于500元,那么老板最多能购进A型文具多少只?