题目内容
【题目】如图,C、D是直线AB上两点,DE平分∠CDF,∠ACE=60°,∠CDF=60°,求∠CED的度数.请完善解答过程,并在括号内填写相应的理论依据.
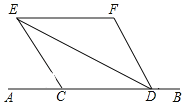
解:∵∠ACE=60°,∠CDF=60°,(已知)
∴∠ACE=∠CDF.(等量代换)
∴ ∥ ,( )
∴∠CED=∠ ,( )
∵DE平分∠CDF,(已知)
∴∠EDF=![]() ∠CDF=
∠CDF=![]() ×60°=30°.( )
×60°=30°.( )
∴∠CED=30°.(等量代换)
【答案】CE,DF,同位角相等,两直线平行,FDE,两直线平行,内错角相等,角平分线的定义.
【解析】
根据等量代换和同位角相等,两直线平行判定CE∥DF,再根据平行线的性质和角平分线的性质求得答案.
∵∠ACE=60°,∠CDF=60°,(已知)
∴∠ACE=∠CDF.(等量代换)
∴ CE ∥ DF ,( 同位角相等,两直线平行 )
∴∠CED=∠ FDE ,( 两直线平行,内错角相等 )
∵DE平分∠CDF,(已知)
∴∠EDF=![]() ∠CDF=
∠CDF=![]() ×60°=30°.( 角平分线的定义 )
×60°=30°.( 角平分线的定义 )
∴∠CED=30°.(等量代换)

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
【题目】为转变教育管理方式并为学校教育教学提供参考,某区240名学生参加2019年国家义务教育质量检测,在测试中随机抽取若干名学生的音乐成绩进行
某区音乐成绩分布表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
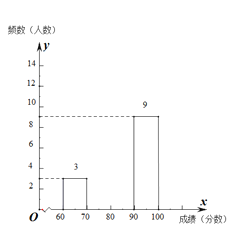
某区音乐成绩频数分布直方图
(1)频数分布表中:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)根据题意,补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,估计该区优秀学生大约有![]() 人.
人.