题目内容
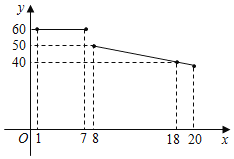
【题目】某水果超市经销一种进价为18元/kg的水果，根据以前的销售经验，该种水果的最佳销售期为20天，销售人员整理出这种水果的销售单价y（元/kg）与第x天（1≤x≤20）的函数图象如图所示，而第x天（1≤x≤20）的销售量m（kg）是x的一次函数，满足下表：
x（天） | 1 | 2 | 3 | … |
m（kg） | 20 | 24 | 28 | … |
（1）请分别写出销售单价y（元/kg）与x（天）之间及销售量m（kg）是x（天）的之间的函数关系式.
（2）求在销售的第几天时，当天的利润最大，最大利润是多少？
【答案】（1）见解析 （2）18天，1936元
【解析】
（1）①销售单价y（元/kg）与x（天）之间根据图像可知是分段函数，当1≤x≤7时，y＝60，当8≤x≤20时，设y＝kx+b（k≠0），代入（8,50）（18,40）解答即可；②设销售量m（kg）是x（天）的之间的函数关系式m＝ax+c，将（1，20）、（2，24）代入解答即可；
（2）设当天的总利润为w，根据利润等于销售单价减去进价之后乘以销售量进行列式，分情况讨论即可得出答案.
（1）①由图像可知当1≤x≤7时，y＝60；
当8≤x≤20时，设y＝kx+b（k≠0），将（8，50）、（18，40）代入得
，解得
，
∴y＝﹣x+58；综上，y＝
；
②设销售量m（kg）是x（天）的之间的函数关系式为m＝ax+c（a≠0），将（1，20）、（2，24）代入得
，解得
，
则m＝4x+16（1≤x≤20）；
（2）设当天的总利润为W，进价为18元/kg，
当1≤x≤7时，
W＝（60﹣18）（4x+16）＝168x+672，
则当x＝7时，W取得最大值，最大值为168×7+672=1848元；
当8≤x≤20时，
W＝（﹣x+58﹣18）（4x+16）
＝﹣4x2+144x+640
=﹣4（x2-36x）+640
=﹣4（x2-36x+182-182）+640
＝﹣4（x﹣18）2+1936，
∴当x＝18时，W取得最大值，最大利润为1936元；
综上，在销售的第18天时，当天的利润最大，最大利润是1936元；
