题目内容
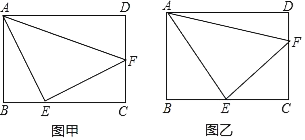
【题目】在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°.如图甲,若EA=EF,则EF=_____;如图乙,若CE=CF,则EF=_____.
【答案】![]()
![]() .
.
【解析】
(1)已知EA=EF,∠EAF=45°,由三角形的内角和得∠AEF=90°,∠AEB+∠FEC=90°,又因∠BAE+∠AEB=90°,等量代换得∠BAE=∠CEF,从而证明△ABE≌△ECF;EF的长可由勾股定理求出.
(2)作辅助线FM 和EN,已知△CEF,构建两个等腰△DEM,△BEN可求出线段DF,AM,FC,BE和AN的长;证明△ANE∽△FMA,再由两个三角形相似的性质求出相似比,解出x的值,由勾股定理(或三角函数)求出EF的长.
解:(1)如图甲所示:

∵EA=EF,
∴△AEF是等腰直角三角形,∠EAF=∠EFA,
∵∠EAF=45°,
∴∠EFA=45°,
又∵在△AEF中,∠EAF+∠EFA+∠AEF=180°,
∴∠AEF=180°﹣45°﹣45°=90°,
又∵∠AEB+∠AEF+∠FEC=180°,
∴∠AEB+∠FEC=90°,
又∵△ABE中,∠B+∠BAE+∠AEB=180°,
∠B=90°,
∴∠BAE+∠AEB=90°,
∴∠BAE=∠CEF,
在△ABE和△ECF中
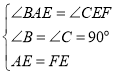 ,
,
∴△ABE≌△ECF(AAS)
∴AB=EC,BE=CF,
又∵AB=3,BC=4,
∴EC=3,CF=1,
在Rt△CEF中,由勾股定理得:
![]()
故答案为![]() .
.
(2)如图乙所示:
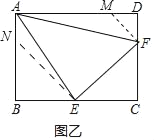
作DM=DF,BN=BE,分别交AD,AB于点M和点N,设MD=x,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,
∴∠BNE=45°,∠DMF=90°,
又∵∠BNE+∠ENA=180°,∠FMD+∠FMA=180°,
∴∠ENA=135°,∠FMA=135°,
又∵∠EAF=45°,∠BAD=∠BAE+∠EAF+∠FAD=90°,
∴∠BAE+∠FAD=45°,
∵∠BAE+∠NEA=45°,
在△ANE和△FMA中
![]() ,
,
∴△ANE∽△FMA
∴![]() ;
;
又∵MD=x,∴DF=x,
∵CE=CF,AB=3,BC=4,
∴FC=EC=3﹣x,BE=BC-CE=4-(3-x)=x+1,AN=2﹣x,
∴ ,
,
解得:x=2![]() ﹣4或x=﹣2
﹣4或x=﹣2![]() ﹣4(舍去),
﹣4(舍去),
∴FC=3﹣(2![]() ﹣4)=7﹣2
﹣4)=7﹣2![]() ,
,
∴EF=![]() FC=
FC=![]() (7﹣2
(7﹣2![]() )=7
)=7![]() ﹣4
﹣4![]() .
.
故答案为7![]() ﹣4
﹣4![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
满意度 | 人数 | 所占百分比 |
非常满意 | 12 | 10% |
满意 | 54 | m |
比较满意 | n | 40% |
不满意 | 6 | 5% |

根据图表信息,解答下列问题:
(1)本次调查的总人数为______,表中m的值为_______;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.