题目内容
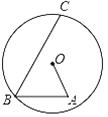
【题目】如图,在⊙O内有折线OABC,点B、C在圆上,点A在⊙O内,其中OA=4cm,BC=10cm,∠A=∠B=60°,则AB的长为_______.
【答案】6
【解析】
延长AO交BC于D,过O作BC的垂线,设垂足为E,根据∠A、∠B的度数易证得△ABD是等边三角形,设AB的长为xcm,由此可表示出OD、BD和DE的长;在Rt△ODE中,根据∠ODE的度数,可得出OD=2DE,进而可求出x的值.
解:延长AO交BC于D,作OE⊥BC于E,
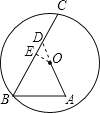
设AB的长为xcm,
∵∠A=∠B=60°,∴∠ADB=60°,
∴△ADB为等边三角形;
∴BD=AD=AB=xcm;
∵OE⊥BC,
∴BE=![]() BC=5cm,
BC=5cm,
∴DE=(x-5)cm,OD=(x-4)cm,
又∵∠ADB=60°,∴∠DOE=30°,
∴DE=![]() OD,
OD,
∴x-5=![]() (x-4),
(x-4),
解得:x=6.
故答案为:6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
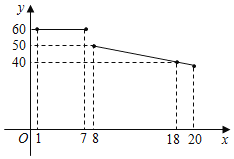
【题目】某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) | 1 | 2 | 3 | … |
m(kg) | 20 | 24 | 28 | … |
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式.
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?