题目内容
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，根据图象回答下列问题：
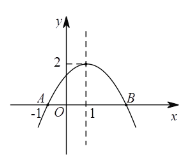
（1）点B的坐标为 ；
（2）y随x的增大而减小的自变量x的取值范围为 ；
（3）方程ax2+bx+c=0的两个根为 ；
（4）不等式ax2+bx+c＜0的解集为 .
【答案】（1）（3，0）；（2）x＞1；（3）x1=-1，x2=3；（4）x＜-1或x＞3.
【解析】
（1）由图象可得：A、B到直线x=1的距离相等，根据A的坐标，即可求出B点坐标；
（2）利用图象得出函数对称轴进而得出y随x的增大而减小的自变量x的取值范围；
（3）根据方程ax2+bx+c=0，即图象与x轴交点，进而得出方程的两个根；
（4）利用不等式ax2+bx+c＜0，即对应图象x轴下方的部分x的取值范围即可得出答案．
解：（1）由图象可得：A、B到直线x=1的距离相等，
∵A（-1，0）
∴B点坐标为：（3，0）
故答案为：（3，0）；
（2）由图象可得：y随x的增大而减小的自变量x的取值范围是：x＞1；
故答案为：x＞1；
（3）∵方程ax2+bx+c=0，即图象与x轴交点，
∴方程ax2+bx+c=0的两个根是：x1=-1，x2=3；
故答案为：x1=-1，x2=3；
（4）由图象可得：不等式ax2+bx+c＜0的解集是：x＜-1或x＞3；
故答案为：x＜-1或x＞3．
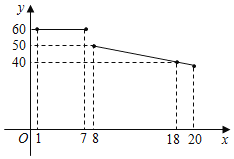
【题目】某水果超市经销一种进价为18元/kg的水果，根据以前的销售经验，该种水果的最佳销售期为20天，销售人员整理出这种水果的销售单价y（元/kg）与第x天（1≤x≤20）的函数图象如图所示，而第x天（1≤x≤20）的销售量m（kg）是x的一次函数，满足下表：
x（天） | 1 | 2 | 3 | … |
m（kg） | 20 | 24 | 28 | … |
（1）请分别写出销售单价y（元/kg）与x（天）之间及销售量m（kg）是x（天）的之间的函数关系式.
（2）求在销售的第几天时，当天的利润最大，最大利润是多少？
