Question

【题目】定义：在平面直角坐标系中，图形G上点P(x,y)的纵坐标y与其横坐标x的差y－x称为P点的“坐标差”，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”

(1)①点A(1,3) 的“坐标差”为 。

②抛物线y=－x2+3x+3的“特征值”为 。

(2)某二次函数y=－x2+bx+c(c≠0) 的“特征值”为1，点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等。

①直接写出m= (用含c的式子表示)

②求此二次函数的表达式。

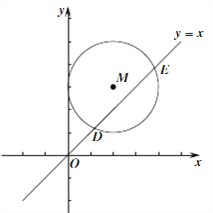
(3)如图，在平面直角坐标系xOy中，以M(2,3)为圆心，2为半径的圆与直线y=x相交于点D、E请直接写出⊙M的“特征值”为 。

Answer 1

【答案】（1）① 2； ② 4； （2）① m= －c ; ②

；（3）

【解析】试题分析：

（1）①由题中所给“坐标差”的定义即可得到点A（1，3）的坐标差；

②由坐标差的定义可得：二次函数y=－x2+3x+3图象上点的坐标差为： ，将此关系式配方即可求得y-x的最大值，从而得到抛物线y=－x2+3x+3的“特征值”；

（2）①由题意可得：0-m=c-0，由此可得：m=-c；

②由m=-c可得点B的坐标为（-c，0），把点B的坐标代入中可得，由可得，即；再由的特征值为1可得： ，两者即可解得b何c的值，由此即可得到二次函数的解析式；

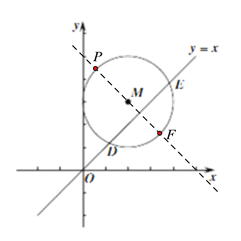
（3）如图，过点M作直线PF⊥DE，交⊙M于点P和F，由已知条件易得直线PF的解析式为y=-x+5；由直线y=x上的所有点的坐标差为0，且坐标平面内在直线y=x的右侧距离直线y=x越远的点的坐标差越大可知在⊙M上距离直线y=x最远的点是点P，设点P的坐标为（x，y）由点P到M的距离为2，可得到关于x、y的方程，和y=-x+5组合即可解得点P的坐标，这样就可得到⊙M的特征值了.

试题解析：

（1）① ∵点A的坐标为（1，3），

∴点A的坐标差为：3-1= 2；

② ∵二次函数的解析式为：y=－x2+3x+3，

∴该二次函数图象上所有点的坐标差都满足： ，

∵，即该二次函数图象上点的坐标差的最大值为4，

∴该二次函数图象的特征值为：4；

（2）① 由已知易得点C的坐标为（0，c），而B的坐标为（m，0），

∴点C的坐标差为：c-0，点B的坐标差为：0-m，

又∵点B与点C的“坐标差”相等，

∴c-0=0-m，

∴m=－c；

② ∵m=－c，

∴B（－c，0），

将其代入 中，

得， ，

∵c≠0，

∴，

∴ ① ，

∴ 的“坐标差”为：

，

∵“特征值”为1，

∴ ②，

将①代入②中，得：

∴ ，

∴抛物线的表达式为 ；

（3）如图，过点M作直线PF⊥DE，交⊙M于点P和F，

∵直线DE的解析式为：y=x，点M的坐标为（2，3），

∴直线PF的解析式为y=-x+5，

∵直线y=x上所有点的坐标差都等于0，而在直线y=x的右侧距离直线y=x越远的点的坐标差就越大，而⊙M上点P距离直线y=x最远，

∴点P的坐标差就是⊙M的“特征值”，

设点P的坐标为（x，y），

∵点P到点M（2，3）的距离为2，

∴有，

又∵点P（x，y）在直线y=-x+5上，

∴，解得： ，

∴对应的： ，

∴点P的坐标为，

∴点P的坐标差为： ，

∴⊙M的“特征值”为： .