ЬтФПФкШн
ЁОЬтФПЁПЮїЙЯОгЊЛЇвд2дЊ/ЧЇПЫЕФМлИёЙКНјХњаЁаЭЮїЙЯЃЌвд3дЊ/ЧЇПЫЕФМлИёГіЪлЃЌУПЬьПЩЪлГі200ЧЇПЫЃЌЮЊСЫДйЯњЃЌИУОгЊЛЇОіЖЈНЕМлЯњЪлЁЃОЕїВщЗЂЯжЃЌетжжаЁаЭЮїЙЯУПНЕМл0.1дЊ/ЧЇПЫЃЌУПЬьПЩЖрЪлГі40ЧЇПЫ.СэЭтЃЌУПЬьЕФЗПзтЕШЙЬЖЈГЩБОЙВ24дЊЁЃИУОгЊЛЇвЊЯыУПЬьгЏРћ200дЊЃЌгІНЋУПЧЇПЫаЁаЭЮїЙЯЕФЪлМлНЕЕЭЖрЩйдЊ?
ЃЈ1ЃЉШєЩшгІНЋУПЧЇПЫЕФЪлМлНЕЕЭxдЊЃЌФЧУДУПЧЇПЫЕФРћШѓЮЊ_____дЊЃЌНЕМлКѓКЮЬьЪлГіЪ§СПЮЊ______ЧЇПЫЃЛ
ЃЈ2ЃЉЧыдкЕк(1)аЁЬтЕФЛљДЁЩЯЃЌСаГіЗНГЬАбДЫЬтНтД№ЭъећЁЃ
ЁОД№АИЁПЃЈ1ЃЉ1-xЃЌ200+400xЃЛЃЈ2ЃЉгІНЋУПЧЇПЫаЁаЭЮїЙЯЕФЪлМлНЕЕЭ0.3дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнетжжаЁаЭЮїЙЯУПНЕМл0.1дЊ/ЧЇПЫЃЌУПЬьПЩЖрЪлГі40ЧЇПЫПЩжБНгЕУГіДњЪ§ЪНЃЛ
ЃЈ2ЃЉЩшгІНЋУПЧЇПЫаЁаЭЮїЙЯЕФЪлМлНЕЕЭxдЊЃЎФЧУДУПЧЇПЫЕФРћШѓЮЊЃКЃЈ3-2-xЃЉЃЌгЩгкетжжаЁаЭЮїЙЯУПНЕМлO.1дЊ/ЧЇПЫЃЌУПЬьПЩЖрЪлГі40ЧЇПЫЃЎЫљвдНЕМлxдЊЃЌдђУПЬьЪлГіЪ§СПЮЊЃК200+![]() ЧЇПЫЃЎ
ЧЇПЫЃЎ
БОЬтЕФЕШСПЙиЯЕЮЊЃКУПЧЇПЫЕФРћШѓЁСУПЬьЪлГіЪ§СП-ЙЬЖЈГЩБО=200ЃЎ
ЃЈ1ЃЉ
ЩшгІНЋУПЧЇПЫаЁаЭЮїЙЯЕФЪлМлНЕЕЭxдЊЃЎФЧУДУПЧЇПЫЕФРћШѓЮЊЃКЃЈ3-2-xЃЉ=(1-x)дЊЃЌгЩгкетжжаЁаЭЮїЙЯУПНЕМлO.1дЊ/ЧЇПЫЃЌУПЬьПЩЖрЪлГі40ЧЇПЫЃЎЫљвдНЕМлxдЊЃЌдђУПЬьЪлГіЪ§СПЮЊЃК200+![]() =ЃЈ200+400xЃЉЧЇПЫ.
=ЃЈ200+400xЃЉЧЇПЫ.
ЙЪЬюЃК1-x ЃЛ 200+400x
ЃЈ2ЃЉИљОнЬтвтЃЌЕУЃЈ1-xЃЉЃЈ200+400xЃЉ-24=200ЃЎ
НтетИіЗНГЬЃЌЕУx1=0.2ЃЌx2=0.3ЃЎ
вђЮЊЮЊСЫДйЯњЙЪx=0.2ВЛЗћКЯЬтвтЃЌЩсШЅЃЌ
Ёрx=0.3ЃЎ
Д№ЃКгІНЋУПЧЇПЫаЁаЭЮїЙЯЕФЪлМлНЕЕЭ0.3дЊЃЎ

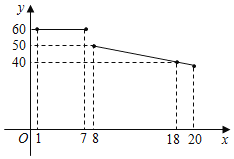
ЁОЬтФПЁПФГЫЎЙћГЌЪаОЯњвЛжжНјМлЮЊ18дЊ/kgЕФЫЎЙћЃЌИљОнвдЧАЕФЯњЪлОбщЃЌИУжжЫЎЙћЕФзюМбЯњЪлЦкЮЊ20ЬьЃЌЯњЪлШЫдБећРэГіетжжЫЎЙћЕФЯњЪлЕЅМлyЃЈдЊ/kgЃЉгыЕкxЬьЃЈ1ЁмxЁм20ЃЉЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌЖјЕкxЬьЃЈ1ЁмxЁм20ЃЉЕФЯњЪлСПmЃЈkgЃЉЪЧxЕФвЛДЮКЏЪ§ЃЌТњзуЯТБэЃК
xЃЈЬьЃЉ | 1 | 2 | 3 | Ё |
mЃЈkgЃЉ | 20 | 24 | 28 | Ё |
ЃЈ1ЃЉЧыЗжБ№аДГіЯњЪлЕЅМлyЃЈдЊ/kgЃЉгыxЃЈЬьЃЉжЎМфМАЯњЪлСПmЃЈkgЃЉЪЧxЃЈЬьЃЉЕФжЎМфЕФКЏЪ§ЙиЯЕЪН.
ЃЈ2ЃЉЧѓдкЯњЪлЕФЕкМИЬьЪБЃЌЕБЬьЕФРћШѓзюДѓЃЌзюДѓРћШѓЪЧЖрЩйЃП