题目内容
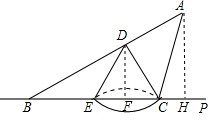
如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过底面圆的圆心,其高为2
m,底 面半径为2m.某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m.
面半径为2m.某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距平面的高度.
| 3 |
 面半径为2m.某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m.
面半径为2m.某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m.(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距平面的高度.
(1)过点D作DF垂直BC于点F.
由题意,得DF=2
,EF=2,BE=4.
在Rt△DFB中,tan∠B=
=
=
,
所以∠B=30°;
(2)过点A作AH垂直BP于点H.
∵∠ACP=2∠B=60°,
∴∠BAC=30°,
∴AC=BC=8,
在Rt△ACH中,AH=AC•Sin∠ACP=8×
=4
,
即光源A距平面的高度为4
m.
由题意,得DF=2
| 3 |
在Rt△DFB中,tan∠B=
| DF |
| BF |
2
| ||
| 2+4 |
| ||
| 3 |
所以∠B=30°;
(2)过点A作AH垂直BP于点H.
∵∠ACP=2∠B=60°,
∴∠BAC=30°,
∴AC=BC=8,
在Rt△ACH中,AH=AC•Sin∠ACP=8×
| ||
| 2 |
| 3 |
即光源A距平面的高度为4
| 3 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 1,
1,