题目内容
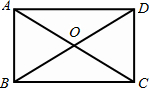
如图，矩形ABCD中，对角线AC、BD相交于点0，∠AOB=60°，AB=5，则AD的长是（ ）
A．5
| B．5
| C．5 | D．10 |
因为在矩形ABCD中，所以AO=
AC=
BD=BO，
又因为∠AOB=60°，所以△AOB是等边三角形，所以AO=AB=5，
所以BD=2AO=10，
所以AD2=BD2-AB2=102-52=75，
所以AD=5
．
故选A．
| 1 |
| 2 |
| 1 |
| 2 |
又因为∠AOB=60°，所以△AOB是等边三角形，所以AO=AB=5，
所以BD=2AO=10，
所以AD2=BD2-AB2=102-52=75，
所以AD=5
| 3 |
故选A．
练习册系列答案
相关题目
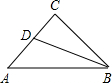
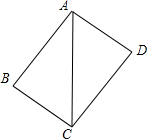
同一条直线上．求电视塔OC的高度以及此人所在位置点P的铅直高度．（测倾器的高度忽略不计，结果保留根号形式）
面半径为2m．某光源位于点A处，照射圆锥体在水平面上留下的影长BE=4m．