Question

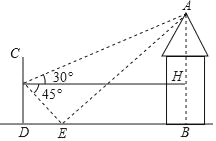
【题目】为了测量休闲凉亭AB的高度，某数学兴趣小组在水平地面D处竖直放置一个标杆CD，并在地面上水平放置一个平面镜E，使得B、E、D在同一水平线上，如图所示．该小组在标杆的F处通过平面镜E恰好观测到凉亭顶端A，在F处测得凉亭A顶端的仰角为30°，平面镜E的俯角为45°，FD＝2米，求休闲凉亭AB的高度．（结果保留根号）

Answer 1

【答案】休闲凉亭AB的高度为（4+2）米．

【解析】

设AB为x米，根据正切的定义列式计算，得到答案．

解：如图所示，由题意可得：DF＝BH＝2米，FH＝DB，

∵∠HFE＝∠FED＝∠AEB＝45°，∠FDE＝∠AHF＝∠ABD＝90°，∠AFH＝30°，

∴∠DFE＝∠FED＝45°，∠AEB＝∠EAB＝45°，

∴DE＝DF＝2米，EB＝AB，

设休闲凉亭AB的高度为x米，则EB＝AB＝x米，

∴FH＝DB＝（x+2）米，

在Rt△AFH中，tan∠AFH＝，

，

∴x＝4+2，

答：休闲凉亭AB的高度为（4+2）米．