题目内容
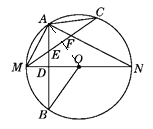
【题目】如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为![]() 上一点,且
上一点,且![]() ,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③
,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③![]() ;④∠ACM+∠ANM=∠MOB;⑤AE=
;④∠ACM+∠ANM=∠MOB;⑤AE=![]() MF.
MF.
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
【答案】D
【解析】根据垂径定理,由AB⊥MN可知AD=DB, ![]() ,故①③正确;根据直径所对的圆周角为直角,可由MN为直径,得到∠MAN=90°,故③正确;
,故①③正确;根据直径所对的圆周角为直角,可由MN为直径,得到∠MAN=90°,故③正确;
如图,
连接OA,由![]() ,得到∠MOB=∠MOA=2∠ACM=∠ACM+∠ANM,故④正确;
,得到∠MOB=∠MOA=2∠ACM=∠ACM+∠ANM,故④正确;
由![]() ,
, ![]() ,可得
,可得![]() ,所以可得∠AME=∠MAE,根据等角对等边,得到AE=ME,然后根据∠EAF+∠MAE=90°,等量代换得∠EFA+∠AME=90°,然后根据等角的余角相等,得到∠EAF=∠EFA,即AE=EF,然后可根据AE=EF=EM得到AE=
,所以可得∠AME=∠MAE,根据等角对等边,得到AE=ME,然后根据∠EAF+∠MAE=90°,等量代换得∠EFA+∠AME=90°,然后根据等角的余角相等,得到∠EAF=∠EFA,即AE=EF,然后可根据AE=EF=EM得到AE=![]() MF,故⑤正确.
MF,故⑤正确.
故选:D.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】2018年4月23日,第23个世界读书日.为了推进中华传统文化教育,营造浓郁的读书氛围,我区某学校举办了“让读书成为习惯,让书香飘满校园”主题活动,为此特为每个班级订购了一批新的图书.初二年级两个班订购图书情况如下表:
老舍文集(套) | 四大名著(套) | 总费用(元) | |
初二(1)班 | 4 | 2 | 480 |
初二(2)班 | 2 | 3 | 520 |
(1)求老舍文集和四大名著每套各是多少元;
(2)学校准备再购买老舍文集和四大名著共10套,总费用不超过700元,问学校有哪几种购买方案.