题目内容
【题目】已知某商品的进价为每件40元．现在的售价是每件60元．每星期可卖出300件．市场调查反映：如调整价格，每涨价一元．每星期要少卖出10件；每降价一元，每星期可多卖出18件．如何定价才能使利润最大？
【答案】答：定价为65元时可获得最大利润，最大利润为6250元.
【解析】
设每星期所获利润为y，然后讨论：若每件涨价x元或每件降价x元，根据一星期利润等于每件的利润×销售量分别得到y=(60-40+x)(300-10x)或y=(60-40-x)(300+18x)，然后把他们配成抛物线顶点式，利用抛物线的最值问题即可得出答案.
解：设每涨价x元，获得的总利润为y元
y=(60-40+x)(300-10x)
=(20+x)(300-10x)
=-10x2+100x+6000
=-10(x-5)2+6250(0≤x≤30)
当x=5时，y的值最大，最大值为6250，此时定价为：60+5=65（元）；
设每涨价x元，获得的总利润为
元
=(20-x)(300+18x)
=-18x2+60x+6000
=-18
(0≤x≤20)
当x=
时，的值最大，最大值为6050，此时定价为：
（元）
综上所述，定价为65元时可获得最大利润，最大利润为6250元.
智慧小复习系列答案【题目】4月23日为世界阅读日，为响应党中央“倡导全民阅读，建设书香会”的号召，某校团委组织了一次全校学生参加的“读书活动”大赛为了解本次赛的成绩，校团委随机抽取了部分学生的成绩(成绩
取整数，总分100分)作为本进行统计，制成如下不完整的统计图表(频数频率分布表和频数分布直方图)：
成绩 | 频数(人) | 频率 |
| 10 | 0.05 |
| 30 | 0.15 |
| 40 |
|
|
| 0.35 |
| 50 | 0.25 |
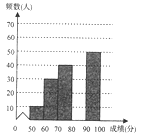
根据所给信息，解答下列问题：
(1)抽取的样本容量是 ；
，
；
(2)补全频数分布直方图；这200名学生成绩的中位数会落在 分数段；
(3)全校有1200名学生参加比赛，若得分为90分及以上为优秀，请你估计全校参加比赛成绩优秀的学生人数．
