题目内容
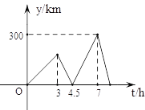
【题目】如图1,已知直线y=a与抛物线![]() 交于A、B两点(A在B的左侧),交y轴于点C
交于A、B两点(A在B的左侧),交y轴于点C
(1)若AB=4,求a的值
(2)若抛物线上存在点D(不与A、B重合),使![]() ,求a的取值范围
,求a的取值范围
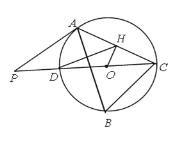
(3)如图2,直线y=kx+2与抛物线交于点E、F,点P是抛物线上的动点,延长PE、PF分别交直线y=-2于M、N两点,MN交y轴于Q点,求QM·QN的值。
图1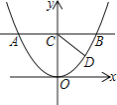 图2
图2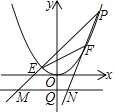
【答案】(1)![]() ;(2)
;(2)![]() ;(3)8
;(3)8
【解析】
(1)将两个函数解析式联立,解一元二次方程求得A、B的横坐标,进而表示出AB,即可解答;
(2)由(1)可得CD=![]() AB=
AB=![]() ,设D
,设D![]() ,过点D作DH⊥y轴于点H,利用勾股定理可知
,过点D作DH⊥y轴于点H,利用勾股定理可知![]() ,进而得到
,进而得到![]() ,得到
,得到![]() ,根据函数图象可知
,根据函数图象可知![]() ,即可求得a的取值范围;
,即可求得a的取值范围;
(3)设E(![]() ),F(
),F(![]() ),P(
),P(![]() ),分别表示EP和FP的解析式,当
),分别表示EP和FP的解析式,当![]() 时,求得
时,求得![]() ,
,![]() ,联立
,联立![]() 和y=kx+2,得到
和y=kx+2,得到![]() ,利用一元二次方程根与系数的关系得到
,利用一元二次方程根与系数的关系得到![]() ,代入
,代入![]() 即可解答.
即可解答.
(1)联立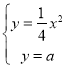 ,
,
∴![]() ,解得:
,解得:![]()
∴![]()
∴![]()
(2)由(1)知AB=![]() ,
,
∴CD=![]() AB=
AB=![]()
设D![]()

过点D作DH⊥y轴于点H,则![]()
∴![]()
∴![]()
又![]()
∴![]()
∴![]()
又![]()
∴![]()
∴![]()
(3)设E(![]() ),F(
),F(![]() ),P(
),P(![]() )
)
EP解析式为![]()
将P,E代入可得:![]()
当![]() 时,可求
时,可求![]() ,
,
同理可求FP的解析式为![]()
![]()
又联立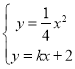 得:
得:![]()
∴![]()
∴![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目