题目内容
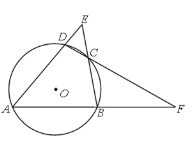
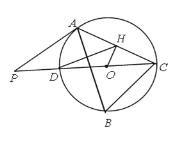
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若OH⊥AC,OH=1,求DH的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据同弧所对的圆心角是圆周角的2倍得到∠AOC的大小,再根据边角关系证明∠PAO是直角,从而证明出PA是⊙O的切线(2)要求DH的长,先根据已知条件证明△CAD是直角三角形,进而可以得到结果.
(1)连接AO
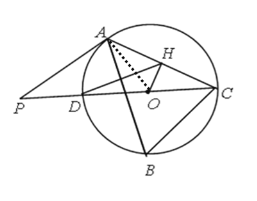
∵ 在⊙O中,∠B=60° ∴ ∠AOC=2∠B=120°
∴ ∠AOD=180°-∠AOC=60°
∵OA=OC ∴∠OCA=∠OAC=30°
∵AP=AC ∴∠APC=∠ACO=30°
∴∠PAO=180°-∠AOD-∠APC=90°
∵点A在⊙O上 ∴PA是⊙O的切线.
(2)连接AD
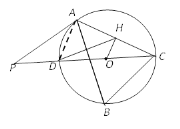
∵ 在⊙O中,OH⊥AC
∴AH=HC
∵ 在⊙O中,DC为直径
∴∠DAC=90°
∵ AH=HC,OD=OC
∴OH是△CAD的中位线
∴AD=2OH=2
∵在Rt△OCH中 ∴tan∠OCH=![]() ∴HC=
∴HC=![]() ∴AH=CH=
∴AH=CH=![]()
∵在Rt△HAD中 ∴HD=![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】近视镜镜片的焦距![]() (单位:米)是镜片的度数
(单位:米)是镜片的度数![]() (单位:度)的函数,下表记录了一组数据:
(单位:度)的函数,下表记录了一组数据:
| … | 100 | 250 | 400 | 500 | … |
| … | 1.00 | 0.40 | 0.25 | 0.20 | … |
(1)在下列函数中,符合上述表格中所给数据的是_________;
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)利用(1)中的结论计算:当镜片的度数为200度时,镜片的焦距约为________米.