题目内容
【题目】某公司销售智能机器人，售价每台为10万元，进价y与销售量x的函数关系式如图所示。
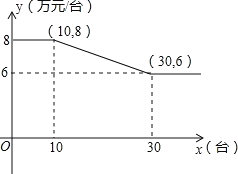
(1)当x=10时，公司销售机器人的总利润为___万元；
(2)当10x30时，求出y与x的函数关系式；
(3)问：销售量为多少台时，公司销售机器人的总利润为37.5万元。
【答案】（1）20；（2）
；（3）销售量为15台时，公司销售机器人的总利润为37.5万元.
【解析】
（1）由“总利润=单台利润×销售数量”结合图象即可得出结论；
（2）设y与x之间的函数关系式为y=kx+b，由函数图象找出点的坐标，再利用待定系数法即可求出结论；
（3）设销售量为m台时，公司销售机器人的总利润为37.5万元．分析销售利润为37.5万元时，销售台数m的范围，再结合此时进价y与x的函数关系式得出销售m台时的进价，再由“总利润=单台利润×销售数量”即可得出关于m的一元二次方程，解方程即可得出结论..
(1)当x=10时,公司销售机器人的总利润为10×（10—8）=20(万元).
故答案为：20.
(2)设y与x之间的函数关系式为y=kx+b，
∵函数图象过点（10，8）（30，6）
∴有
，解得：
∴当10<x<30时，y与x的函数关系式为
(3)设销售量为m台时，公司销售机器人的总利润为37.5万元.
∵37.5>20，
∴m>10，
又∵m为正整数，
∴4m≠37.5.
∴只有在10<m<30内，公式销售机器人的总利润才有可能为37.5万元.
依题意得：m[10(
)]=37.5，
解得：
，
(舍去).
答：销售量为15台时，公司销售机器人的总利润为37.5万元.
练习册系列答案
相关题目
