��Ŀ����
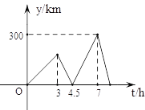
����Ŀ����һ����ֱ�Ĺ�·����A��B���أ��ס�������������Ҫ��A���ͻ���B�أ��׳��ȴ�A�س���������ʻ��3Сʱ���ҳ���A�س���������ͬһ·��������ʻ�����ҳ�����B�غ����̰�ԭ�ٷ��أ��ڷ���;�еڶ�����׳��������׳�������ʱ���Ϊt (Сʱ)������֮��ľ����Ϊy��ǧ�ף���y��t�ĺ�����ϵ��ͼ��ʾ�����ҳ��ڶ�����׳�����ʱ���׳�����A��___ǧ��.
���𰸡�495
��������
ͨ���۲�ͼ���Եó��������ٶȵı�����ϵ���ҳ�����B�ص����õ�ʱ�䣬��׳��ٶ�Ϊxkm/h,���������г�������������ٶȣ�����һ����������������õ�ʱ�䣬�Ӷ��õ��׳���ʱ��A�صľ���.
��ͼ���֪���׳�����4.5hʱ���ҳ����˼׳�������1.5h�������ҳ��ٶ��Ǽ׳���3��.
���ҳ���ʻ��7-3��4Сʱʱ���������300km�����������뿪ʼ��С��˵����ʱ�ҳ�����B�ؿ�ʼ����.
��׳�ÿСʱ��xkm,���ҳ�ÿСʱ��3xkm.��
(7-4.5)(3x-x)=300
���x=60,3x=180
���ҳ���ʼ���غ�th�����ڶ�����������������ã�
��180+60��t=300
���t=1.25
��׳���ʻ��·��Ϊ����7+1.25����60��495km.
��ʱ�׳���A��495ǧ��.
�ʴ�Ϊ��495.

 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�����Ŀ��ijһ�죬ˮ����Ӫ��������1600Ԫ��ˮ�������г�����⨺��Һ�â����50ǧ�ˣ����ٵ�ˮ���г�ȥ������֪⨺��Һ�â������������ۺ����ۼ������ʾ��
Ʒ�� | ⨺��� | â�� |
������ | 20 | 40 |
���ۼ� | 26 | 50 |
![]() ��������⨺��Һ�â��������ǧ�ˣ�
��������⨺��Һ�â��������ǧ�ˣ�
![]() ���⨺��Һ�â��ȫ�����꣬��������Ǯ��
���⨺��Һ�â��ȫ�����꣬��������Ǯ��
����Ŀ������ij��ͬѧС�������ѧϰ�����ľ��飬̽������![]() ��ͼ������ʣ�����������̽�����̣��벹��������
��ͼ������ʣ�����������̽�����̣��벹��������
��1������![]() ���Ա�����ȡֵ��Χ�� ;
���Ա�����ȡֵ��Χ�� ;
��2���±��Ǻ���![]() ���Ա���
���Ա���![]() �ļ����Ӧֵ��
�ļ����Ӧֵ��
| -3 | -2 | -1 | 0 | 1 | 3 | 4 | 5 | 6 | 7 |
| |
|
| 0.6 | m | 1 | 1.5 | 3 | n | 1.5 | 1 | 0.75 | 0.6 |
|
��m= ,n= ��
��3����ƽ��ֱ������ϵxoy�У���ȫ�˺�����ͼ��:
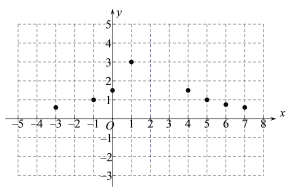
��4�����ݺ���ͼ��ֱ��д������ʽ![]() �Ľ⼯ ;
�Ľ⼯ ;
��5��������![]() �뺯��y��x��kͼ����������ͬ�Ľ��㣬��k��ȡֵ��Χ�� .
�뺯��y��x��kͼ����������ͬ�Ľ��㣬��k��ȡֵ��Χ�� .