题目内容
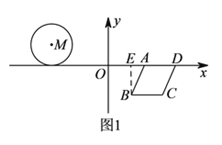
【题目】如图,⊙![]() 与菱形
与菱形![]() 在平面直角坐标系中,点
在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 在点
在点![]() 的右侧.
的右侧.


(![]() )求菱形
)求菱形![]() 的周长.
的周长.
(![]() )若⊙
)若⊙![]() 沿
沿![]() 轴向右以每秒
轴向右以每秒![]() 个单位长度的速度平移,菱形
个单位长度的速度平移,菱形![]() 沿
沿![]() 轴向左以每秒
轴向左以每秒![]() 个单位长度的速度平移,设菱形移动的时间为(
个单位长度的速度平移,设菱形移动的时间为(![]() 秒),当⊙
秒),当⊙![]() 与
与![]() 相切,且切点为
相切,且切点为![]() 的中点时,连接
的中点时,连接![]() ,求
,求![]() 的值及
的值及![]() 的度数.
的度数.
(![]() )在(
)在(![]() )的条件下,当点
)的条件下,当点![]() 与
与![]() 所在的直线的距离为
所在的直线的距离为![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)菱形的周长为8;(2)![]() ,
, ![]() ;(3)
;(3)![]()
【解析】试题分析:(1)过点B作BE⊥AD,垂足为E.由点A和点B的坐标可知:BE=![]() ,AE=1,依据勾股定理可求得AB的长,从而可求得菱形的周长;(2)记 M与x轴的切线为F,AD的中点为E.先求得EF的长,然后根据路程=时间×速度列出方程即可;平移的图形如图3所示:过点B作BE⊥AD,垂足为E,连接MF,F为 M与AD的切点.由特殊锐角三角函数值可求得∠EAB=60°,依据菱形的性质可得到∠FAC=60°,然后证明△AFM是等腰直角三角形,从而可得到∠MAF的度数,故此可求得∠MAC的度数;(3)如图4所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.先求得∠MAE=30°,依据特殊锐角三角函数值可得到AE的长,然后依据3t+2t=5-AE可求得t的值;如图5所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.依据菱形的性质和切线长定理可求得∠MAE=60°,然后依据特殊锐角三角函数值可得到EA=
,AE=1,依据勾股定理可求得AB的长,从而可求得菱形的周长;(2)记 M与x轴的切线为F,AD的中点为E.先求得EF的长,然后根据路程=时间×速度列出方程即可;平移的图形如图3所示:过点B作BE⊥AD,垂足为E,连接MF,F为 M与AD的切点.由特殊锐角三角函数值可求得∠EAB=60°,依据菱形的性质可得到∠FAC=60°,然后证明△AFM是等腰直角三角形,从而可得到∠MAF的度数,故此可求得∠MAC的度数;(3)如图4所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.先求得∠MAE=30°,依据特殊锐角三角函数值可得到AE的长,然后依据3t+2t=5-AE可求得t的值;如图5所示:连接AM,过点作MN⊥AC,垂足为N,作ME⊥AD,垂足为E.依据菱形的性质和切线长定理可求得∠MAE=60°,然后依据特殊锐角三角函数值可得到EA=![]() ,最后依据3t+2t=5+AE.列方程求解即可.
,最后依据3t+2t=5+AE.列方程求解即可.
试题解析:( ![]() )如图1所示:过点
)如图1所示:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
∴菱形的周长![]() .
.
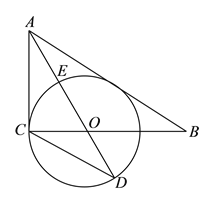
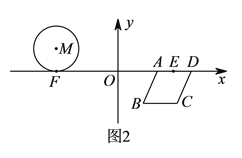
(![]() )如图2所示,⊙
)如图2所示,⊙![]() 与
与![]() 轴的切线为
轴的切线为![]() ,
, ![]() 中点为
中点为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() 为
为![]() 中点,
中点,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
解得![]() .
.
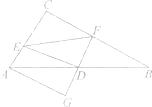
平移的图形如图3所示:过点![]() 作
作![]() ,
,
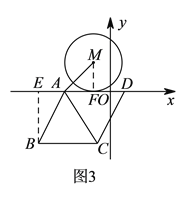
垂足为![]() ,连接
,连接![]() ,
, ![]() 为⊙
为⊙![]() 与
与![]() 切点,
切点,
∵由(![]() )可知,
)可知, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∵![]() 为
为![]() 切线,
切线,
∴![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
(![]() )如图4所示:连接
)如图4所示:连接![]() ,过点作
,过点作![]() ,垂足为
,垂足为![]() ,作
,作![]() ,垂足为
,垂足为![]() ,
,
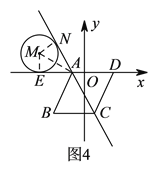
∵四边形![]() 为菱形,
为菱形, ![]() ,
,
∴![]() .
.
∵![]() 、
、![]() 是圆
是圆![]() 的切线
的切线
∴![]() ,
,
∵![]() 。
。
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
如图5所示:连接![]() ,过点作
,过点作![]() ,垂足为
,垂足为![]() ,作
,作![]() ,垂足为
,垂足为![]() ,
,
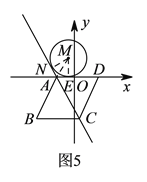
∵四边形![]() 为菱形,
为菱形, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 、
、![]() 是圆
是圆![]() 的切线,
的切线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,当![]() 或
或![]() 时,圆
时,圆![]() 与
与![]() 相切.
相切.

 名校课堂系列答案
名校课堂系列答案