题目内容
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)猜想PM与PN的数量关系及位置关系,请直接写出结论;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.

【答案】(1)PM=PN,PM⊥PN,理由见解析;(2)理由见解析;(3)PM=kPN;理由见解析
【解析】试题分析:(1)由等腰直角三角形的性质易证△ACE≌△BCD,由此可得AE=BD,再根据三角形中位线定理即可得到PM=PN,由平行线的性质可得PM⊥PN;(2)(1)中的结论仍旧成立,由(1)中的证明思路即可证明;(3)PM=kPN,由已知条件可证明△BCD∽△ACE,所以可得BD=kAE,因为点P、M、N分别为AD、AB、DE的中点,所以PM=![]() BD,PN=
BD,PN=![]() AE,进而可证明PM=kPN.
AE,进而可证明PM=kPN.
试题解析:(1)PM=PN,PM⊥PN,理由如下:
∵△ACB和△ECD是等腰直角三角形, ∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
在△ACE和△BCD中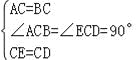 , ∴△ACE≌△BCD(SAS), ∴AE=BD,∠EAC=∠CBD,
, ∴△ACE≌△BCD(SAS), ∴AE=BD,∠EAC=∠CBD,
∵点M、N分别是斜边AB、DE的中点,点P为AD的中点, ∴PM=![]() BD,PN=
BD,PN=![]() AE,
AE,
∴PM=PM, ∵∠NPD=∠EAC,∠MPN=∠BDC,∠EAC+∠BDC=90°, ∴∠MPA+∠NPC=90°,
∴∠MPN=90°, 即PM⊥PN;
(2)∵△ACB和△ECD是等腰直角三角形, ∴AC=BC,EC=CD,∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠ECD+∠BCE. ∴∠ACE=∠BCD. ∴△ACE≌△BCD. ∴AE=BD,∠CAE=∠CBD.
又∵∠AOC=∠BOE,∠CAE=∠CBD, ∴∠BHO=∠ACO=90°.
∵点P、M、N分别为AD、AB、DE的中点, ∴PM=![]() BD,PM∥BD; PN=
BD,PM∥BD; PN=![]() AE,PN∥AE.
AE,PN∥AE.
∴PM=PN. ∴∠MGE+∠BHA=180°. ∴∠MGE=90°. ∴∠MPN=90°. ∴PM⊥PN.
(3)PM=kPN
∵△ACB和△ECD是直角三角形, ∴∠ACB=∠ECD=90°. ∴∠ACB+∠BCE=∠ECD+∠BCE.
∴∠ACE=∠BCD. ∵BC=kAC,CD=kCE, ∴![]() =k. ∴△BCD∽△ACE. ∴BD=kAE.
=k. ∴△BCD∽△ACE. ∴BD=kAE.
∵点P、M、N分别为AD、AB、DE的中点, ∴PM=![]() BD,PN=
BD,PN=![]() AE. ∴PM=kPN.
AE. ∴PM=kPN.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案