题目内容
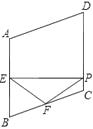
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.

【答案】(1)证明见解析;(2)AB⊥BC时,四边形AEOF正方形.
【解析】
(1)根据中点的定义及菱形的性质可得BE=DF,∠B=∠D,BC=CD,利用SAS即可证明△BCE≌△DCF;
(2)由中点的定义可得OE为△ABC的中位线,根据三角形中位线的性质可得OE//BC,根据正方形的性质可得∠AEO=90°,根据平行线的性质可得∠ABC=∠AEO=90°,即可得AB⊥BC,可得答案.
(1)∵四边形ABCD是菱形,点E,O,F分别是边AB,AC,AD的中点,
∴AB=BC=CD=AD,∠B=∠D,
∵点E、F分别是边AB、AD的中点,
∴BE=![]() AB,DF=
AB,DF=![]() AD,
AD,
∴BE=DF,
在△BCE和△DCF中,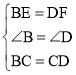 ,
,
∴△BCE≌△DCF.
(2)AB⊥BC,理由如下:
∵四边形AEOF是正方形,
∴∠AEO=90°,
∵点E、O分别是边AB、AC的中点,
∴OE为△ABC的中位线,
∴OE//BC,
∴∠B=∠AEO=90°,
∴AB⊥BC.

【题目】甲,乙两人是NBA联盟凯尔特人队的两位明星球员,两人在前五个赛季的罚球
命中率如下表所示:
甲球员的命中率(%) | 87 | 86 | 83 | 85 | 79 |
乙球员的命中率(%) | 87 | 85 | 84 | 80 | 84 |
(1)分别求出甲,乙两位球员在前五个赛季罚球的平均命中率;
(2)在某场比赛中,因对方球员技术犯规需要凯尔特人队选派一名队员进行罚球,你认为甲,乙两位球员谁来罚球更好?(请通过计算说明理由)
【题目】2013年是一个让人记忆犹新的年份,雾霾天气持续笼罩我国大部分地区,口罩市场出现热销,某旗舰网店用8000元购进甲、乙两种型号的口罩,销售完后共获利2800元,进价和售价如下表:
品名 价格 | 甲型口罩 | 乙型口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种型号口罩各多少袋?
(2)该网店第二次以原价购进甲、乙两种型号口罩,购进乙种型号口罩袋数不变,而购进甲种型号口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种型号的口罩都售完,要使第二次销售活动获利不少于3680元,乙种型号的口罩最低售价为每袋多少元?