Question

【题目】已知二次函数y＝x2，当a≤x≤b时m≤y≤n，则下列说法正确的是（　　）

A.当n﹣m＝1时，b﹣a有最小值

B.当n﹣m＝1时，b﹣a有最大值

C.当b﹣a＝1时，n﹣m无最小值

D.当b﹣a＝1时，n﹣m有最大值

Answer 1

【答案】B

【解析】

①当b﹣a＝1时，先判断出四边形BCDE是矩形，得出BC＝DE＝b﹣a＝1，CD＝BE＝m，进而得出AC＝n﹣m，即tan＝n﹣m，再判断出0°≤∠ABC＜90°，即可得出n﹣m的范围；

②当n﹣m＝1时，同①的方法得出NH＝PQ＝b﹣a，HQ＝PN＝m，进而得出MH＝n﹣m＝1，而tan∠MHN＝，再判断出45°≤∠MNH＜90°，即可得出结论．

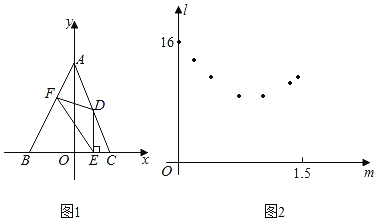
解：①当b﹣a＝1时，如图1，过点B作BC⊥AD于C，

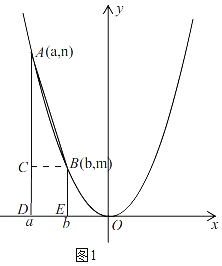
∴∠BCD＝90°，

∵∠ADE＝∠BED＝90°，

∴∠ADO＝∠BCD＝∠BED＝90°，

∴四边形BCDE是矩形，

∴BC＝DE＝b﹣a＝1，CD＝BE＝m，

∴AC＝AD﹣CD＝n﹣m，

在Rt△ACB中，tan∠ABC＝＝n﹣m，

∵点A，B在抛物线y＝x2上，

∴0°≤∠ABC＜90°，

∴tan∠ABC≥0，

∴n﹣m≥0，

即n﹣m无最大值，有最小值，最小值为0，故选项C，D都错误；

②当n﹣m＝1时，如图2，过点N作NH⊥MQ于H，

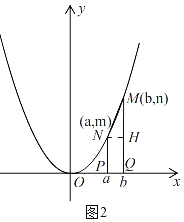
同①的方法得，NH＝PQ＝b﹣a，HQ＝PN＝m，

∴MH＝MQ﹣HQ＝n﹣m＝1，

在Rt△MHQ中，tan∠MNH＝，

∵点M，N在抛物线y＝x2上，

∴m≥0，

当m＝0时，n＝1，

∴点N（0，0），M（1，1），

∴NH＝1，

此时，∠MNH＝45°，

∴45°≤∠MNH＜90°，

∴tan∠MNH≥1，

∴≥1，

∴b﹣a无最小值，有最大值，最大值为1，故选项A错误；

故选：B．