Question

【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．

（1）求证：△ECF∽△GCE；

（2）求证：EG是⊙O的切线；

（3）延长AB交GE的延长线于点M，若tanG=，AH=，求EM的值．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）．

【解析】

试题分析：（1）由AC∥EG，推出∠G=∠ACG，由AB⊥CD推出，推出∠CEF=∠ACD，推出∠G=∠CEF，由此即可证明；

（2）欲证明EG是⊙O的切线只要证明EG⊥OE即可；

（3）连接OC．设⊙O的半径为r．在Rt△OCH中，利用勾股定理求出r，证明△AHC∽△MEO，可得，由此即可解决问题；

试题解析：（1）证明：如图1．∵AC∥EG，∴∠G=∠ACG，∵AB⊥CD，∴，∴∠CEF=∠ACD，∴∠G=∠CEF，∵∠ECF=∠ECG，∴△ECF∽△GCE．

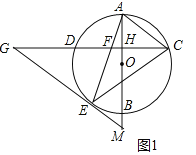
（2）证明：如图2中，连接OE．∵GF=GE，∴∠GFE=∠GEF=∠AFH，∵OA=OE，∴∠OAE=∠OEA，∵∠AFH+∠FAH=90°，∴∠GEF+∠AEO=90°，∴∠GEO=90°，∴GE⊥OE，∴EG是⊙O的切线．

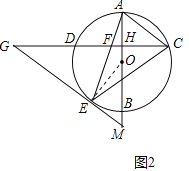
（3）解：如图3中，连接OC．设⊙O的半径为r．

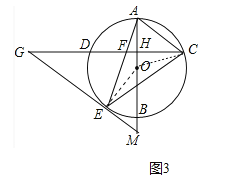
在Rt△AHC中，tan∠ACH=tan∠G==，∵AH=，∴HC=，在Rt△HOC中，∵OC=r，OH=r﹣，HC=，∴，∴r=，∵GM∥AC，∴∠CAH=∠M，∵∠OEM=∠AHC，∴△AHC∽△MEO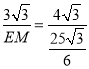，∴，∴，∴EM=．