题目内容
【题目】在边长为3的正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA边上,且满足EB=FC=GD=HA=1,BD分别与HG、HF、EF相交于M、O、N.给出以下结论,
①HO=OF ②0F2=ON·OB③HM=2MG ④S△HOM= ![]() ,其中正确的个数有( )
,其中正确的个数有( )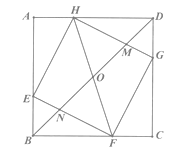
A.1
B.2
C.3
D.4
【答案】D
【解析】解 :∵四边形ABCD是正方形,
∴ AD=BC =AB=CD=3 , ,∠A=∠ABC=∠C=∠ADC=90° ,∠ADB=∠DBC=45° ,
∵EB=FC=GD=HA=1 ,
∴AE==CG=BF=DH=2 ,
∴AEH≌BFE≌CGF≌DHG ,
∴EH=EF=FG=GH ,∠AHE=∠BEF ,
∵∠AEH+∠AHE=90° ,
∴∠AEH+∠BEF=90° ,
∴∠HEF=90°
∴四边形EFGH是正方形 ,
∴∠OFN=45°
∴,∠OFN=∠OBF=45° ,
又∵∠FON=∠BOF ,
∴ONF∽OFB ,
∴ON∶OF=OF∶OB ,
∴0F2=ON·OB ; 故②正确;
在HOD与FOB中 ,
∵,∠ADB=∠DBC ,∠HOD=∠FOB ,HD=BF ,
∴HOD≌FOB ,
∴HO=OF ;故①正确;
∵SHDM∶SDMG=2∶1 ,SHDM∶SDMG=HM∶MG ,
∴HM∶MG =2∶1 ,
∴HM=2MG ;故③正确;
在RtAEH中,∠A=90° ,AH=1 ,AE=2 ,
根据勾股定理EH=![]() ,
,
∵S正方形EFGH=5 ,SHOG=S正方形EFGH=![]() ,
,
又∵SHOM∶SOMG=HM∶MG=2∶1 ,
∴S△HOM=![]() 。故④正确。
。故④正确。
故答案为 :D .
根据正方形的性质得出AD=BC =AB=CD=3 , ,∠A=∠ABC=∠C=∠ADC=90° ,∠ADB=∠DBC=45°,进而得出AE==CG=BF=DH=2 ,从而判断出AEH≌BFE≌CGF≌DHG ,根据全等三角形的性质得出EH=EF=FG=GH ,∠AHE=∠BEF ,根据三角形的内角和及同角的余角相等,平角的定义得出∠HEF=90° ,进而判断出四边形EFGH是正方形 ,根据正方形的性质判断出∠OFN=∠OBF=45° ,进而判断出ONF∽OFB ,根据相似三角形的性质得出0F2=ON·OB ;
根据AAS判断出HOD≌FOB ,根据全等三角形的性质得出HO=OF ;
根据角平分线的性质定理得出HDM与DMG如果分别以DH,DG为底的话,它们的高相等,从而得出SHDM∶SDMG=2∶1 又SHDM∶SDMG=HM∶MG ,HM∶MG =2∶1 ,HM=2MG ;
首先利用勾股定理得出EH的长,进而得出正方形EFGH的面积,根据正方形的性质得出SHOG=S正方形EFGH=![]() ,又SHOM∶SOMG=HM∶MG=2∶1 从而得出答案。
,又SHOM∶SOMG=HM∶MG=2∶1 从而得出答案。

【题目】为改善生态环境,防止水土流失,某村计划在江汉堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
甲林场 | 乙林场 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过1000棵时 | 4元/棵 | 不超过2000棵时 | 4元/棵 |
超过1000棵的部分 | 3.8元/棵 | 超过2000棵的部分 | 3.6元/棵 |
设购买白杨树苗x棵,到两家林场购买所需费用分别为y甲(元)、y乙(元).
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?