��Ŀ����
����Ŀ����ͼ����֪������Y=ax2+bxһ3��X���ཻ��A(һ1��0)��B(3��0)��PΪ�������ϵ��������ϵĵ㣮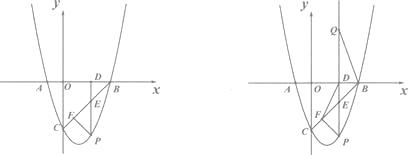
��1����������ߵĺ�����ϵʽ��
��2������P��PD��X���ڵ�D��PD��BC�ڵ�E�����߶�PE�ij������ʱ�����P�����꣮
��3�����߶�PE�ij������ʱ����PF ��BC�ڵ�F������DF��������PD����һ��Q�������PQB=��DFB���������������Ƿ����һ��R��ʹ��S��RBE=S��QBE��������ڣ�ֱ��д��R������ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1���� ����A(һ1��0)��B(3��0)�ֱ����Y=ax2+bxһ3�� ![]()
��� ![]()
��������ߵĺ�����ϵʽΪ y=x2-2x-3 ;
��2���� ����x=0����y=x2-2x-3 ;�ã�y=-3 ,
��C ��0��-3�� ��
��ֱ��BC�Ľ���ʽΪy=kx+b,��C ��0��-3����B(3��0)���ֱ����� ��![]()
��� ![]() ,
,
��ֱ��BC�Ľ���ʽΪy=x-3 ;
��P ��m,m2-2m-3��,
����P��PD��X���ڵ�D��PD��BC�ڵ�E ��
E ��m,m-3�� ,
��PE=(m-3)-(m2-2m-3)=-m2+3m=-(m-![]() )2+
)2+![]() ,
,
�ʵ�m=![]() ʱ��PE���ʱP ��
ʱ��PE���ʱP ��![]() ��-
��-![]() ��
��
��3���� �����߶�PE�ij������ʱ ,P ��![]() ��-
��-![]() �� ��E ��
�� ��E ��![]() ��-
��-![]() �� ��PE =
�� ��PE =![]() ,
,
�� D(![]() ,0) ,
,0) ,
��BD =![]()
��B��3,0�� ��C ��0,3��
��OB=3=OC ��
��OBCΪ����ֱ�������� �����OBC=45�� ,
��RtDBE����ABC=45�� ,DB=![]() ,
,
��BE=![]()
![]() ,��DEB=45�� ,
,��DEB=45�� ,
���PEF=45��
��RtPEF�� ��PEF=45�� PE=![]() ,
,
��EF=![]() ,
,
��BF=![]() ;
;
�ߡ�PQB=DFB ,��DBE=��DEB=45�� ,
��QBE��FDB ,
��DB��BE��BF��QE ,
�� ![]() ��
��![]() =
=![]() ��QE ,
��QE ,
��QE=![]() ,
,
��SBQE=![]() ��QE��DB=
��QE��DB=![]() =
=![]() ;
;
��R����x����ʱ����R ��n,0�� ,BR=|3-n| ,
��SRBE=![]() ,
,
��![]() =
=![]() |3-n|��
|3-n|��![]()
|3-n|=![]()
n1=-![]() n2=
n2=![]() .
.
��R (-![]() ,0) (
,0) (![]() ,0) ;
,0) ;
��R��y���ϵ�ʱ����R��0��z��
SBER=SBRC-SREC
��![]() =
=![]()
![]() 3��|z-3|-
3��|z-3|-![]() ��
��![]() ��|z-3|
��|z-3|
��� z1=![]() ,z2=-
,z2=-![]() ;
;
��R (0,-![]() ) (0,
) (0, ![]() ) ,
) ,
����������R���������0 . ![]() �� ��0��-
�� ��0��- ![]() ����
����![]() ��0���� -
��0���� -![]() ��0��
��0��
����������1���ô���ϵ������������ߵĽ���ʽ ��
��2���������C������꣬���ô���ϵ�������ֱ��BC�Ľ���ʽΪy=x-3 ����P ��m,m2-2m-3��������P��PD��X���ڵ�D��PD��BC�ڵ�E ���Ӷ�E ��m,m-3�� ����PE=(m-3)-(m2-2m-3)=-m2+3m=-(m-![]() )2+
)2+![]() ���Ӷ������m=
���Ӷ������m=![]() ʱ��PE���ʱP ��
ʱ��PE���ʱP ��![]() ��-
��-![]() ����
����
��3���������E �����꣬PE���ȣ������ó�BD�ij��ȣ�����B,C����������жϳ�OBCΪ����ֱ�������Σ��������ݹ��ɶ����ó�BE�ij������ݶԶ�����ȵó���RtPEF�С�PEF=45�㣬���ݹ��ɶ����ó�EF�ij����Ӷ��ó�BF�ij���Ȼ���жϳ�QBE��FDB ,�������������ζ�Ӧ�߳ɱ����г����̣����QE�ij������������ε������ʽ���SBQE����R����x����ʱ����R ��n,0�� ,BR=|3-n| ,����S��RBE=S��QBE�г��������n��ֵ���ó�R������꣬��R��y���ϵ�ʱ����R��0��z�� ��SBER=SBRC-SREC�г��������z��ֵ�������R����y���ϵ�ʱ������꣬�Ӷ��ó�����𰸡�

 ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�