题目内容
【题目】如图，已知△ABC为直角三角形，∠ACB=90°，AC=BC，点A，C在x轴上，点B坐标为（3，m）（m＞0），线段AB与y轴相交于点D，以P（1，0）为顶点的抛物线过点B，D．
（1）求点A的坐标（用m表示）；
（2）求抛物线的解析式；
（3）设点Q为抛物线上点P至点B之间的一动点，连接PQ并延长交BC于点E，连接BQ并延长交AC于点F，试证明：FC（AC+EC）为定值．
【答案】
（1）解：由B（3，m）可知OC=3，BC=m，又△ABC为等腰直角三角形，
∴AC=BC=m，OA=m﹣3，
∴点A的坐标是（3﹣m，0）
（2）解：∵∠ODA=∠OAD=45°
∴OD=OA=m﹣3，
则点D的坐标是（0，m﹣3）．
又抛物线顶点为P（1，0），且过点B、D，
所以可设抛物线的解析式为：y=a（x﹣1）2，
得： 
解得 
∴抛物线的解析式为y=x2﹣2x+1
（3）解：方法一：
证明：过点Q作QM⊥AC于点M，过点Q作QN⊥BC于点N，
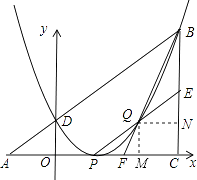
设点Q的坐标是（x，x2﹣2x+1），
则QM=CN=（x﹣1）2，MC=QN=3﹣x．
∵QM∥CE
∴△PQM∽△PEC
∴ 
即 
，得EC=2（x﹣1）
∵QN∥FC
∴△BQN∽△BFC
∴ 
即 
，得 
又∵AC=4
∴FC（AC+EC）= 
[4+2（x﹣1）]= （2x+2）= ×2×（x+1）=8
即FC（AC+EC）为定值8．
方法二：
设Q（t，t2﹣2t+1），B（3，4），
设直线BQ：y=kx+b，
∴lBQ：y=（t+1）x+1﹣3t，
把y=0代入y=（t+1）x+1﹣3t，
∴x= 
，即F（ ，0），
∵P（1，0），Q（t，t2﹣2t+1），
∴lPQ：y=（t﹣1）x+1﹣t，
把x=3代入，∴y=2t﹣2，即E（3，2t﹣2），
∴FC（AC+EC）=（CX﹣FX）（CX﹣AX+EY﹣CY）=（3﹣ ）（4+2t﹣2）=8．
【解析】（1）求A点坐标可先求OA，利用线段之差即可求出；（2）先把抛物线解析式设成顶点式，再把B（3，m)、D点坐标（0，m-3)代入即可；（3） 线段的积可利用相似的性质对应边成比例，转化为其他线段的积.
