题目内容
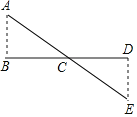
【题目】如图,△AOB是直角三角形,∠AOB=90。 , 0B=2OA,点A在反比例函数 ![]() 的图象上,点B在反比例函数
的图象上,点B在反比例函数 ![]() 的图象上,则k的值是( )
的图象上,则k的值是( )
A.-4
B.4
C.-2
D.2
【答案】A
【解析】解 : 过点A,B作AC⊥x轴于点C,,BD⊥x轴与点D,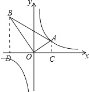
设点A的坐标是(m,n),则AC=n,OC=m.
∵∠AOB=90,
∴∠AOC+∠BOD=90°
∵∠DBO+∠BOD=90°
∴∠DBO=∠AOC.
∵∠BDO=∠ACO=90°
∴△BDO∽△OCA.
∴BD∶OC=OD∶AC=OB∶OA.
∵OB=2OA,
∴BD=2m,OD=2n.
因为点A在反比例函数y=![]() 的图象上,
的图象上,
∴mn=1.
∵点B在反比例函数y=![]() 的图象上,
的图象上,
∴B点的坐标是(2n,2m).
∴k=2n2m=4mn=4.
故答案为 :A 。
设点A的坐标是(m,n),则AC=n,OC=m.首先根据同角的余角相等得出∠DBO=∠AOC.又∠BDO=∠ACO=90° ,从而判断出△BDO∽△OCA.根据相似三角形对应边成比例得出BD∶OC=OD∶AC=OB∶OA.从而得出BD=2m,OD=2n.根据反比例函数比例系数的几何意义得出mn=1.从而得出K的值 。

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目