题目内容
已知,平面直角坐标系上有A(a,0)、B(0,-b)、C(b,0)三点,且a≥b>0,抛物线y=(x-2)(x-m)-(n-2)(n-m).(m,n为常数,且m+2≥2n>0),经过点A和点C,顶点为P
(1)当m,n满足什么关系时,S△AOB最大;
(3)如图,当△ACP为直角三角形时,判断以下命题是否正确:“直角三角形DEF的三个顶点都在这条抛物线上,且DF∥x轴,那么△ACP与△DEF斜边上的高相等”,如果正确请予以证明,不正确请举出反例.
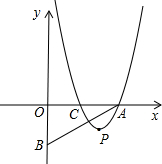
(1)当m,n满足什么关系时,S△AOB最大;
(3)如图,当△ACP为直角三角形时,判断以下命题是否正确:“直角三角形DEF的三个顶点都在这条抛物线上,且DF∥x轴,那么△ACP与△DEF斜边上的高相等”,如果正确请予以证明,不正确请举出反例.

(1)∵y=(x-2)(x-m)-(n-2)(n-m)=(x-n)(x+n-m-2),
又∵m+2≥2n,即m+2-n≥n,
∴点(m+2-n,0)在点(n,0)右边.
又抛物线过A点和C点,
∴a=m+2-n,b=n,
∵S△AOB=
ab=
(m+2-n)n≤
[
(m+2-n)+n]2=
(m+2)2,
当且仅当m+2-n=n时取“=”,此时m+2=2n,
当m+2=2n时,S△AOB最大;
(2)命题正确.
理由:∵当△ACP是直角三角形时,AP⊥CP,且|AC|等于P点到x轴距离的2倍.
又∵抛物线y=(x-n)(x+n-m-2)=[x-
(m+2)]2-
(m+2)2+n(m+2-n),
∴顶点必然在x轴下方,
∴由 2[
(m+2)2-n(m+2-n)]=(m+2-n)-n,
化简得:[(m+2)-2n][(m+2)-(2n+2)]=0,
显然A、C不会是同一点,
∴m+2-n>n,即(m+2)-2n>0,
∴(m+2)-(2n+2)=0,
得:m=2n,
代回原方程有y=(x-n)(x-n-2),
∴点A(n+2,0),点C(n,0),点P(n+1,-1).
假设命题成立,
∵DE∥x轴,
∴点F为Rt△DEF的直角.
令D、E的纵坐标均为y=b,则可求的两点的坐标分别为:D(n+1-
,b),E(n+1+
,b).
设点F坐标为(x0,y0),
∵DF⊥EF,
∴有
•
=-1,
化简得(x0-n-1)2+(y0-b)2=b+1,
又(x0,y0)满足y0=(x0-n)(x0-n-2)=[(x0-n-1)+1][(x0-n-1)-1]=(x0-n-1)2-1,
联立两式消去x0化简得:y02+(1-2b)y0+(b2-b)=0,
求得y0=b或b-1,舍去y0=b,故y0=b-1,
∴F到斜边DE的距离为b-(b-1)=1,这与P到斜边AC距离一样.
综合上述:命题是正确的.
又∵m+2≥2n,即m+2-n≥n,
∴点(m+2-n,0)在点(n,0)右边.
又抛物线过A点和C点,
∴a=m+2-n,b=n,
∵S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
当且仅当m+2-n=n时取“=”,此时m+2=2n,
当m+2=2n时,S△AOB最大;
(2)命题正确.
理由:∵当△ACP是直角三角形时,AP⊥CP,且|AC|等于P点到x轴距离的2倍.
又∵抛物线y=(x-n)(x+n-m-2)=[x-
| 1 |
| 2 |
| 1 |
| 4 |
∴顶点必然在x轴下方,
∴由 2[
| 1 |
| 4 |
化简得:[(m+2)-2n][(m+2)-(2n+2)]=0,
显然A、C不会是同一点,
∴m+2-n>n,即(m+2)-2n>0,
∴(m+2)-(2n+2)=0,
得:m=2n,
代回原方程有y=(x-n)(x-n-2),
∴点A(n+2,0),点C(n,0),点P(n+1,-1).
假设命题成立,
∵DE∥x轴,
∴点F为Rt△DEF的直角.
令D、E的纵坐标均为y=b,则可求的两点的坐标分别为:D(n+1-
| b+1 |
| b+1 |
设点F坐标为(x0,y0),
∵DF⊥EF,
∴有
| y0-b | ||
x0-(n+1-
|
| y0-b | ||
x0-(n+1+
|
化简得(x0-n-1)2+(y0-b)2=b+1,
又(x0,y0)满足y0=(x0-n)(x0-n-2)=[(x0-n-1)+1][(x0-n-1)-1]=(x0-n-1)2-1,
联立两式消去x0化简得:y02+(1-2b)y0+(b2-b)=0,
求得y0=b或b-1,舍去y0=b,故y0=b-1,
∴F到斜边DE的距离为b-(b-1)=1,这与P到斜边AC距离一样.
综合上述:命题是正确的.

练习册系列答案
相关题目
 ,与x轴相交于点F.
,与x轴相交于点F. ,(0,2).
,(0,2).
 垂直的边AD长为x米,
垂直的边AD长为x米, A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.
A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.