题目内容
如图,EF是一面长18米的墙,用总长为32米的木栅栏(图中的虚线)围一个矩形场地,中间还要隔成三块.设与墙头 垂直的边AD长为x米,
垂直的边AD长为x米,
(1)用含x的代数式表示AB的长为______米;
(2)若要围成的矩形面积为60米2,求AB的长;
(3)当x为何值时,矩形的面积S最大?是多少?
 垂直的边AD长为x米,
垂直的边AD长为x米,(1)用含x的代数式表示AB的长为______米;
(2)若要围成的矩形面积为60米2,求AB的长;
(3)当x为何值时,矩形的面积S最大?是多少?
(1)∵与墙头垂直的边AD长为x米,四边形ABCD是矩形,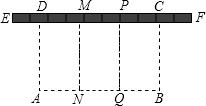
∴BC=MN=PQ=x米,
∴AB=32-AD-MN-PQ-BC=32-4x(米),
故答案为:32-4x;
(2)根据题意得:x(32-4x)=60,
解得:x=3或x=5,
当x=3时,AB=32-4x=20>18(舍去);
当x=5时,AB=32-4x=12(米),
∴AB的长为12米;
(3)根据题意得:S=x(32-4x)=-4x2+32x=-4(x-4)2+64,
∴当x=4时,S最大,最大值为64米2,
∴当x为4时,矩形的面积S最大,是64米2.

∴BC=MN=PQ=x米,
∴AB=32-AD-MN-PQ-BC=32-4x(米),
故答案为:32-4x;
(2)根据题意得:x(32-4x)=60,
解得:x=3或x=5,
当x=3时,AB=32-4x=20>18(舍去);
当x=5时,AB=32-4x=12(米),
∴AB的长为12米;
(3)根据题意得:S=x(32-4x)=-4x2+32x=-4(x-4)2+64,
∴当x=4时,S最大,最大值为64米2,
∴当x为4时,矩形的面积S最大,是64米2.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
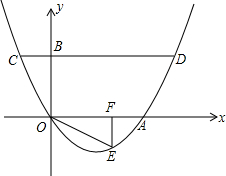


 位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.
位,平移后抛物线的顶点坐标记作A,直线x=3与平移后的抛物线相交于B,与直线OA相交于C.