题目内容
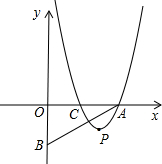
如图,抛物线y=-
x2+x+3与x轴相交于点A、B,与y轴相交于点C,顶点为点D,对称轴l与直线BC相交于点E ,与x轴相交于点F.
,与x轴相交于点F.
(1)求直线BC的解析式;
(2)设点P为该抛物线上的一个动点,以点P为圆心,r为半径作⊙P
①当点P运动到点D时,若⊙P与直线BC相交,求r的取值范围;
②若r=
,是否存在点P使⊙P与直线BC相切?若存在,请求出点P的坐标;若不存在,请说明理由.
提示:抛物线y=ax2+bx+x(a≠0)的顶点坐标(-
,
),对称轴x=-
.
| 1 |
| 4 |
 ,与x轴相交于点F.
,与x轴相交于点F.(1)求直线BC的解析式;
(2)设点P为该抛物线上的一个动点,以点P为圆心,r为半径作⊙P
①当点P运动到点D时,若⊙P与直线BC相交,求r的取值范围;
②若r=
| 4 |
| 5 |
| 5 |
提示:抛物线y=ax2+bx+x(a≠0)的顶点坐标(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
(1)抛物线y=-
x2+x+3中,
令y=0,得0=-
x2+x+3,
解得x=-2,x=6;
令x=0,得y=3;
∴A(-2,0),B(6,0),C(0,3);
设直线BC的解析式为y=kx+b,则有:
,
解得
∴直线BC的解析式为:y=-
x+3;
(2)由抛物线的解析式知:y=-
(x-2)2+4,
即D(2,4);
当x=2时,y=-
x+3=-1+3=2,
即E(2,2);
∴EF=DE=2,BF=4;
①过D作DG⊥BC于G,则△DEG∽△BEF;
∴DE:GE=BF:EF=2:1,即DG=2GE;
Rt△DGE中,设GE=x,则DG=2x,
由勾股定理,得:GE2+DG2=DE2,
即:4x2+x2=4,
解得x=
;
∴DG=2x=
;
故D、P重合时,若⊙P与直线BC相切,则r>DG,即r≥
;
②存在符合条件的P点,且P点坐标为:P1(2,4),P2(4,3),P3(3+
,
),P4(3-
,
);
过点F作FM⊥BC于M;
∵DE=EF=2,则Rt△DGE≌Rt△FME;
∴FM=DG=r=
;
分别过D、F作直线m、n平行于直线BC,则直线m与直线BC、直线n与直线BC之间的距离都等于r;
所以P点必为直线m、n与抛物线的交点;
设直线m的解析式为:y=ax+h,由于直线m与直线BC平行,则a=-
;
∴-
×2+h=4,h=5,
即直线m的解析式为y=-
x+5;
同理可求得直线n的解析式为:y=-
x+1;
联立直线m与抛物线的解析式,
得:
,
解得
,
;
∴P1(2,4),P2(4,3);
同理,联立直线n与抛物线的解析式可求得:P3(3+
,
),P4(3-
,
);
故存在符合条件的P点,且坐标为:P1(2,4),P2(4,3),P3(3+
,
),P4(3-
,
).
| 1 |
| 4 |
令y=0,得0=-
| 1 |
| 4 |
解得x=-2,x=6;
令x=0,得y=3;
∴A(-2,0),B(6,0),C(0,3);
设直线BC的解析式为y=kx+b,则有:
|
解得
|
∴直线BC的解析式为:y=-
| 1 |
| 2 |
(2)由抛物线的解析式知:y=-
| 1 |
| 4 |
即D(2,4);
当x=2时,y=-
| 1 |
| 2 |
即E(2,2);
∴EF=DE=2,BF=4;
①过D作DG⊥BC于G,则△DEG∽△BEF;

∴DE:GE=BF:EF=2:1,即DG=2GE;
Rt△DGE中,设GE=x,则DG=2x,
由勾股定理,得:GE2+DG2=DE2,
即:4x2+x2=4,
解得x=
2
| ||
| 5 |
∴DG=2x=
4
| ||
| 5 |
故D、P重合时,若⊙P与直线BC相切,则r>DG,即r≥
4
| ||
| 5 |
②存在符合条件的P点,且P点坐标为:P1(2,4),P2(4,3),P3(3+
| 17 |
3-
| ||
| 2 |
| 17 |
3+
| ||
| 2 |
过点F作FM⊥BC于M;
∵DE=EF=2,则Rt△DGE≌Rt△FME;
∴FM=DG=r=
4
| ||
| 5 |
分别过D、F作直线m、n平行于直线BC,则直线m与直线BC、直线n与直线BC之间的距离都等于r;
所以P点必为直线m、n与抛物线的交点;
设直线m的解析式为:y=ax+h,由于直线m与直线BC平行,则a=-
| 1 |
| 2 |
∴-
| 1 |
| 2 |
即直线m的解析式为y=-
| 1 |
| 2 |
同理可求得直线n的解析式为:y=-
| 1 |
| 2 |
联立直线m与抛物线的解析式,
得:
|
解得
|
|
∴P1(2,4),P2(4,3);
同理,联立直线n与抛物线的解析式可求得:P3(3+
| 17 |
3-
| ||
| 2 |
| 17 |
3+
| ||
| 2 |
故存在符合条件的P点,且坐标为:P1(2,4),P2(4,3),P3(3+
| 17 |
3-
| ||
| 2 |
| 17 |
3+
| ||
| 2 |

练习册系列答案
相关题目

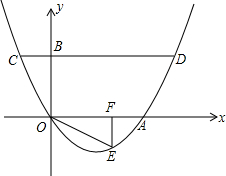


 点C的横坐标为1,
点C的横坐标为1,