Question

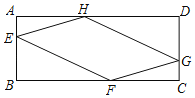
【题目】如图，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动，且满足，．

(1)求证：；

(2)试判断四边形EFGH的形状，并说明理由．

(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系，并说明理由．

Answer 1

【答案】(1)证明见解析；(2)四边形EFGH是平行四边形，理由见解析；(3)四边形EFGH的周长一半大于或者等于矩形ABCD一条对角线长度，理由见解析.

【解析】

（1）根据全等三角形的判定定理SAS证得结论；
（2）由（1）中全等三角形的性质得到：EH=GF，同理可得FE=HG，即可得四边形EFGH是平行四边形；
（3）由 轴对称--最短路径问题得到：四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．

解：(1)∵四边形ABCD是矩形，

∴．

∴在与中，，

∴；

(2)∵由(1)知，，则，同理证得，则，

∴四边形EFGH是平行四边形；

(3) 四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．

理由如下：作G关于BC的对称点G′，连接EG′，可得EG′的长度就是EF+FG的最小值．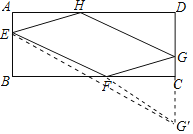

连接AC，
∵CG′=CG=AE，AB∥CG′，
∴四边形AEG′C为平行四边形，
∴EG′=AC．
在△EFG′中，∵EF+FG′≥EG′=AC，
∴四边形EFGH的周长一半大于或等于矩形ABCD一条对角线长度．