题目内容
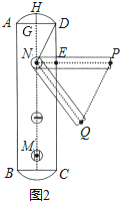
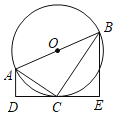
【题目】如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD=![]() ,CE=3,则
,CE=3,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() πC.
πC.![]() πD.
πD.![]() π
π
【答案】D
【解析】
连接OC,由AB是⊙O的直径得到∠ACB=90°,由此证得∠DAC=∠ECB,再证△ADC∽△CEB,列对应边成比例由此求出∠ABC=30°,根据直线DE与⊙O相切于点C求出∠ACD=∠ABC=30°求出AB得到半径,再利用弧长公式计算.
解:连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,BE⊥DE,
∴∠DAC+∠ACD=90°,
∴∠DAC=∠ECB,
∵∠ADC=∠CEB=90°,
∴△ADC∽△CEB,
∴![]() ,即
,即![]() ,
,
∵tan∠ABC=![]() ,
,
∴∠ABC=30°,
∴AB=2AC,∠AOC=60°,
∵直线DE与⊙O相切于点C,
∴∠ACD=∠ABC=30°,
∴AC=2AD=2![]() ,
,
∴AB=4![]() ,
,
∴⊙O的半径为2![]() ,
,
∴![]() 的长为:
的长为:![]() =
=![]() π,
π,
故选:D.

练习册系列答案
相关题目