��Ŀ����
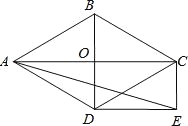
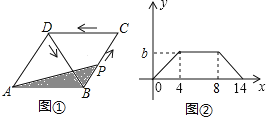
����Ŀ��ʵ���������������ѧϰ�ı��ε����֪ʶʱ����ʶ��ƽ���ı��Ρ����Ρ����Ρ������ε�һЩ������ı��Σ����������ó߹���ͼ�ķ������������֮�����ϵ����ͼ������ABCD�У�AB��4��BC��6����ABC��60�����������������
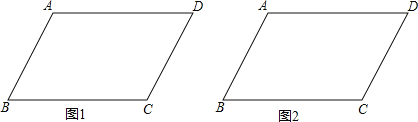
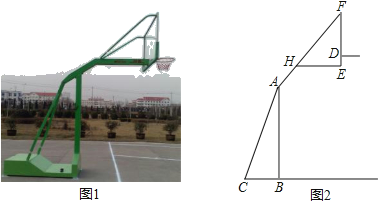
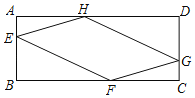
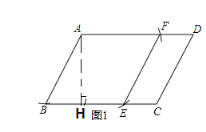
��1����ͼ1����һ�����Σ�ʹ�õ�A��BΪ�������ε�2�����㣬����2����������ABCD�ı��ϣ���ͼ2����һ�����Σ�ʹ��B��DΪ�������ε�2�����㣬����2����������ABCD�ı��ϣ����߹���ͼ��������ͼ�ۼ�����д������
��2������ͼ���·����ߴ�ֱ��д���㰴��1����Ҫ�����������ε������
���𰸡���1�������������2��ͼ1��8![]() ��ͼ2��
��ͼ2��![]() ��
��
��������
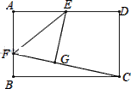
��1������������������ȵ����ʽ��л�ͼ���������εĶԽ����ഹֱƽ�ֵ����ʻ�ͼ��
��2�����������ʽ����������Եĵ��ɣ�ͼ1����AH��BC,����ΪH�������������ʺ��ɶ������BH��AH���ɣ�ͼ2����BH��AD,����ΪH�����ı���BEDFΪ���Σ�����BE=ED=BF=x���������Ǻ�����ϵ�ɵ�AH,BH�����ݹ��ɶ����ɵã�8-x��2+��![]() ��2=x2�������BF��
��2=x2�������BF��
��1����ͼ��ʾ������ABEF������BEDFΪ����
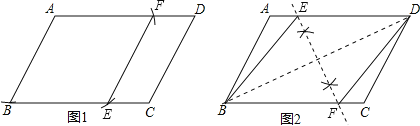
��2��ͼ1��
��AH��BC,����ΪH
��Ϊ�ı���ABEF������
����BE=AB=4
����ABC��60��
���ԡ�HAB��30��
����BH=![]()
����AH=![]()
�����ı���ABEF������ǣ�
![]()
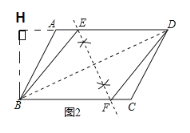
ͼ2��
��BH��AD,����ΪH
��Ϊ�ı���BEDFΪ����
���Կ���BE=ED=BF=x��
��Ϊƽ���ı���ABCD�С�ABC��60����
���ԡ�HAB=��ABC��60��
����BH=ABsin60��![]() ��AH= ABcos60��
��AH= ABcos60��![]()
����HE=HD-ED=2+6-x=8-x
������Rt��HBE �У���HB2+HE2=BE2�ɵ�
��8-x��2+��![]() ��2=x2
��2=x2
���x=![]()
����BF=![]()
��������BEDF������ǣ�
![]()

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ����ѧ�ڣ���������չ����ǡͬѧ���꣬Ʒʫ���������л���ͳʫ�ʴ����![]() С��ͳ���˰༶30��ͬѧ���·ݵ�ʫ�ʱ����������������������ʾ��
С��ͳ���˰༶30��ͬѧ���·ݵ�ʫ�ʱ����������������������ʾ��
ʫ������ | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
���� | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
��ô��30��ͬѧ���·�ʫ�ʱ�����������������λ���ֱ���![]() ����
����![]()
A. 11��7 B. 7��5 C. 8��8 D. 8��7