题目内容
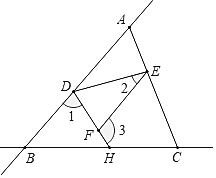
【题目】已知：如图，在ABCD中，AE⊥BC，CF⊥AD，E，F分别为垂足．
（1）求证：△ABE≌△CDF；
（2）求证：四边形AECF是矩形．
【答案】（1）证明见解析；（2）证明见解析．
【解析】
（1）由平行四边形的性质得出∠B=∠D，AB=CD，AD∥BC，由已知得出∠AEB=∠AEC=∠CFD=∠AFC=90°，由AAS证明△ABE≌△CDF即可；
（2）证出∠EAF=∠AEC=∠AFC=90°，即可得出结论．
（1）证明：∵四边形ABCD是平行四边形，
∴∠B＝∠D，AB＝CD，AD∥BC，
∵AE⊥BC，CF⊥AD，
∴∠AEB＝∠AEC＝∠CFD＝∠AFC＝90°，
在△ABE和△CDF中，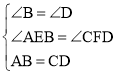
，
∴△ABE≌△CDF（AAS）；
（2）证明：∵AD∥BC，AE⊥BC
∴∠EAF＝∠AEB＝90°，
CF⊥AD
∴∠EAF＝∠AEC＝∠AFC＝90°，
∴四边形AECF是矩形．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
