Question

【题目】在平面直角坐标系xOy中，抛物线经过点A（-3，4）．

（1）求b的值；

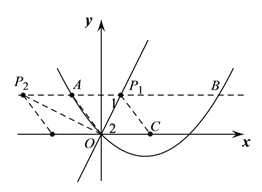
（2）过点A作轴的平行线交抛物线于另一点B，在直线AB上任取一点P，作点A关于直线OP的对称点C；

①当点C恰巧落在轴时，求直线OP的表达式；

②连结BC，求BC的最小值．

Answer 1

【答案】（1）-3；（2）①OP的表达式为或，②BC的最小值为．

【解析】试题分析：（1）把点A坐标代入解析式即可得；

（2）①由对称性可知OA=OC，AP=CP，由AP∥OC，可得∠1=∠2，再根据轴对称可得∠AOP=∠2，从而得∠AOP=∠1，得到AP=AO，再根据A点坐标即可得AP的长，从而得P点的坐标，利用待定系数法即可得解析式；

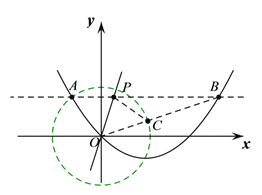
②以O为圆心，OA长为半径作⊙O，连接BO，交⊙O于点C，此时BC的值最小.

试题解析：（1）∵抛物线经过点A（-3，4），

令x=-3，代入，则，

∴b=-3；

（2）①由对称性可知OA=OC，AP=CP，

∵AP∥OC，∴∠1=∠2，

又∵∠AOP=∠2，∴∠AOP=∠1，

∴AP=AO，

∵A（-3，4），

∴AO=5，∴AP=5，

∴P1（2，4），

同理可得P2（-8，4），

∴OP的表达式为或；

②以O为圆心，OA长为半径作⊙O，连接BO，交⊙O于点C，此时BC值最小，

把y=4代入，解得：x1=12，x2=-3，∴B（12，4），

∴OB=， ∴BC的最小值为．