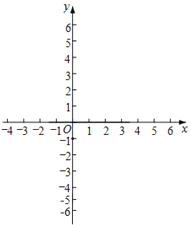题目内容
【题目】如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴是直线x=﹣2．关于下列结论：①ab<0；②b2﹣4ac>0；③9a﹣3b+c>0；④b﹣4a=0；⑤ 方程ax2+bx=0的两个根为 x1=0，x2=﹣4，其中正确的结论有（ ）
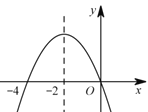
A.②③B.②③④C.②③⑤D.②③④⑤
【答案】D
【解析】
根据二次函数的图像与性质即可得出答案.
由图像可知，a＜0，b＜0，故①错误；
∵图像与x轴有两个交点
∴
，故②正确；
当x=-3时，y=9a﹣3b+c，在x轴的上方
∴y=9a﹣3b+c>0，故③正确；
∵对称轴
∴b-4a=0，故④正确；
由图像可知，方程ax2+bx=0的两个根为 x1=0，x2=﹣4，故⑤正确；
故答案选择D.
练习册系列答案
相关题目
【题目】有这样一个问题：探究函数y＝(x﹣1)(x﹣2)(x﹣3)的图象与性质.小东对函数y＝(x﹣1)(x﹣2)(x﹣3)的图象与性质进行了探究.下面是小东的探究过程，请补充完成：
(1)函数y＝(x﹣1)(x﹣2)(x﹣3)的自变量x的取值范围是_______；
(2)下表是y与x的几组对应值.
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | m | ﹣24 | ﹣6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
①m＝_____；
②若M(﹣7，﹣720)，N(n，720)为该函数图象上的两点，则n＝_____；
(3)在平面直角坐标系xOy中，A(xA，yA)，B(xB，﹣yA)为该函数图象上的两点，且A为2≤x≤3范围内的最低点，A点的位置如图所示.
①标出点B的位置；
②画出函数y＝(x﹣1)(x﹣2)(x﹣3)(0≤x≤4)的图象.
③写出直线y＝
x﹣1与②中你画出图象的交点的横坐标之和为______.
