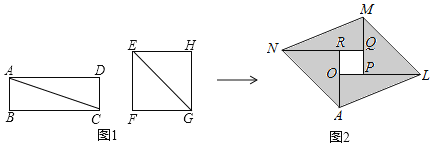题目内容
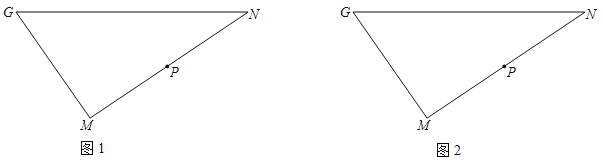
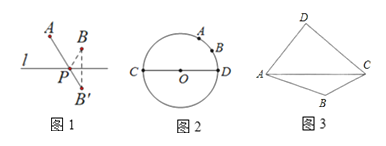
【题目】(理论学习)学习图形变换中的轴对称知识后,我们容易在直线![]() 上找到点
上找到点![]() ,使
,使![]() 的值最小,如图
的值最小,如图![]() 所示,根据这一理论知识解决下列问题:
所示,根据这一理论知识解决下列问题:
(1)(实践运用)如图![]() ,已知
,已知![]() 的直径
的直径![]() 为
为![]() ,弧
,弧![]() 所对圆心角的度数为
所对圆心角的度数为![]() ,点
,点![]() 是弧
是弧![]() 的中点,请你在直径
的中点,请你在直径![]() 上找一点
上找一点![]() ,使
,使![]() 的值最小,并求
的值最小,并求![]() 的最小值.
的最小值.
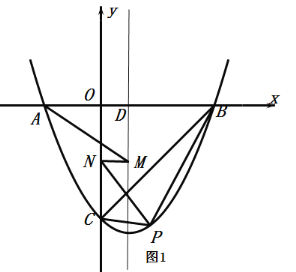
(2)(拓展延伸)在图![]() 中的四边形
中的四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(尺规作图,保留作图痕迹,不必写出作法).
.(尺规作图,保留作图痕迹,不必写出作法).
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
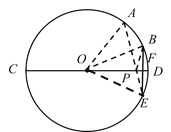
(1)先作B关于CD的对称点E,连接OA、OB、OE、AE,AE交CD于P,求出∠AOE=90°,求出△AOE是等腰直角三角形,根据勾股定理求出AE,即可求出答案;
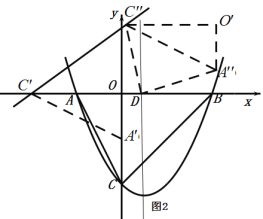
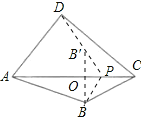
(2)画点B关于AC的对称点B′,延长DB′交AC于点P.则点P即为所求.
解:(1)作点![]() 关于
关于![]() 的对称点
的对称点![]() ,则点
,则点![]() 在圆上,连接
在圆上,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 最短,连接
最短,连接![]() .
.
![]() ,
,![]() 是弧
是弧![]() 的中点,
的中点,
![]() ,
,
![]()
![]() 关于
关于![]() 的对称点
的对称点![]() ,
,![]()
又![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
(2)如图,作点![]() 关于
关于![]() 的对称点B′,连接DB′交
的对称点B′,连接DB′交![]() 于点
于点![]() ,
,
由AC是BB′的垂直平分线,可得∠APB=∠APD.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
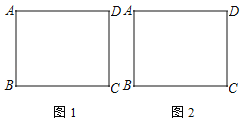
【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:

材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.