题目内容
【题目】已知,在△ABC中,∠BAC=90°,AB=AC,CE平分∠ACB交AB于点E。
(1)∠B= 度.
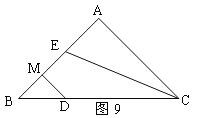
(2)如图9,若点D在斜边BC上,DM垂直平分BE,垂足为M。求证:BD=AE;
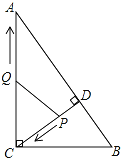
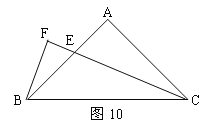
(3)如图10,过点B作BF⊥CE,交CE的延长线与点F。若CE=6,求△BEC的面积。
【答案】(1)45°,(2)证明见解析;(3)4.
【解析】
【试题分析:(1)连接DE,由∠BAC=90°,AB=AC,可得∠B=45°,
(2)由DM垂直平分BE,可得BD=DE,进而判断△BDE是等腰直角三角形,所以ED⊥BD,然后由角平分线的性质可得ED=AE,根据等量代换可得BD=AE;
(3)延长BF,CA,交与点G,由CE平分∠ACB,可得∠ACE=∠BCE,由BF⊥CE,可得∠BFC=∠GFC=90°,然后由三角形内角和定理可得:∠GBC=∠G,进而可得BC=GC,然后由等腰三角形的三线合一,可得BF=FG=![]() BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
试题解析:(1)连接ED,如图1,

∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
(2)∵DM垂直平分BE,
∴BD=DE,
∴∠BED=∠EBD=45°,
∴∠EDC=∠EBD+∠BED=90°,
∵CE平分∠ACB,∠BAC=90°,∠EDC=90°,
∴ED=EA,
∴BD=AE;
(3)延长BF,CA,交与点G,如图2所示,

∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵BF⊥CE,
∴∠BFC=∠GFC=90°,
∴∠GBC=∠G,
∴BC=GC,
∴BF=FG=![]() BG,
BG,
即BG=2BF=4,
∵∠GFC=∠GAB=90°,
∴∠ACF+∠BGC=90°,∠ABG+∠BGC=90°,
∴∠ACF=∠ABG,
在△ACE和△ABG中,
 ,
,
∴△ACE≌△ABG(SAS),
∴BG=CE,
∴EC=2BF=4,
∴S△ECB=![]() CEBF=
CEBF=![]() ×4×2=4.
×4×2=4.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第![]() (1≤
(1≤![]() ≤90)天的售价与销量的相关信息如下表:
≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.