题目内容
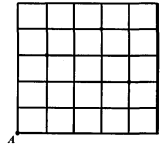
【题目】若干个偶数按每行8个数排成如图所示的阵列：
（1）图中方框内的9个数的和与中间的数有什么关系？
（2）小亮画了一个方框，他所画的方框内9个数的和为360，求这9个数；（直接写出答案）。
（3）小霞也画了一个方框，方框内9个数的和为262，你能写出这9个数吗？如果不能，请说明理由。
【答案】（1）方框内的9个数的和是中间的数的9倍;
（2）这九个数分别为22,24,26,38,40,42,54,56,58;
（3）因为262不能整除9，所以方框中间的数不能用整数表示出来，故不存在这9个数使得和为262．
【解析】
试题分析：（1）根据已知9个数直接求出和即可，进而得出与中间的数的关系；
（2）可设中间的数为
，根据（1）中规律得出这9个数的和的方程，解方程即可求解；
（3）可设中间的数为
，根据（1）中规律得出这9个数的和的方程，解方程即可求解．
试题解析：（1）
所以方框内的9个数的和是中间的数的9倍；
（2）设中间的数为
，依题意得，
解得
所以这九个数分别为22,24,26,38,40,42,54,56,58;
（3）设中间的数为
，依题意得，
解得
262不能整除9，
方框中间的数不能用整数表示出来．故不存在这9个数使得和为262．
【题目】根据下面的两种移动电话计费方式表，考虑下列问题：
月使用费/元 | 主叫限定时间/min | 主叫超时费/（元/min） | 被叫 | |
方式一 | 58 | 150 | 0.25 | 免费 |
方式二 | 88 | 350 | 0.19 | 免费 |
（1）一个月内在本地通话180min，按方式一需要交费多少元？按方式二呢？
（2）对于某一主叫通话时间，是否存在两种方式的计费相等？如果存在，请求出；如果不存在，请说明理由.
【题目】某同学在学习了统计知识后，就下表所列的5种用牙不良习惯对全班每一个同学进行了问卷调查（每个被调查的同学必须选择而且只能在5种用牙不良习惯中选择一项），调查结果如下统计图所示．根据以上统计图提供的信息，回答下列问题：
种类 | A | B | C | D | E |
不良习惯 | 睡前吃水果喝牛奶 | 用牙开瓶盖 | 常喝饮料嚼冰 | 常吃生冷零食 | 磨牙 |
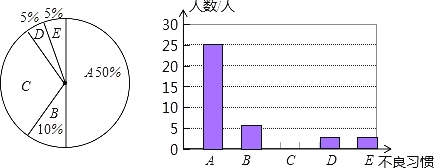
（1）这个班有多少名学生？
（2）这个班中有C类用牙不良习惯的学生多少人？占全班人数的百分比是多少？
（3）请补全条形统计图；
（4）根据调查结果，估计这个年级850名学生中有B类用牙不良习惯的学生多少人？
