题目内容
【题目】如图,是一次函数y=kx+b的图象.
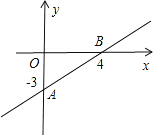
(1)求这个一次函数的解析式?
(2)试判断点P(1,-1)是否在这个一次函数的图象上?
(3)求原点O到直线AB的距离.
【答案】(1)一次函数的解析式y=![]() x-3;(2)不成立,(3)
x-3;(2)不成立,(3)![]() .
.
【解析】试题分析:(1)根据待定系数法即可求解;
(2)把P的坐标代入解析式进行检验即可;
(3)在直角△OAB中,根据勾股定理可以求得AB的长,再根据面积公式即可求解.
试题解析:(1)设函数的解析式为y=kx+b(k≠0),
∵图象与x,y轴交点的坐标分别为(4,0),(0,-3),
∴把两点代入函数解析式得![]() ,解得
,解得 ,
,
故一次函数的解析式y=![]() x-3;
x-3;
(2)把P(1,-1)代入解析式得-1=![]() -3,不成立,
-3,不成立,
故此点不在这个一次函数的图象上;
(3)在△OAB中|OB|=4,|OA|=|-3|=3,由勾股定理得AB2=OA2+OB2,即AB2=32+42,
则AB=5,
设原点O到直线AB的距离为h.则![]() h×|AB|=
h×|AB|=![]() |OA||OB|,
|OA||OB|,
即h=![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,学习委员小兵每周对各小组合作学习的情况进行了综合评分.下表是其中一周的统计数据:
组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
分 值 | 90 | 95 | 90 | 88 | 90 | 92 | 85 |
这组数据的中位数和众数分别是
A. 88,90 B. 90,90 C. 88,95 D. 90,95