题目内容
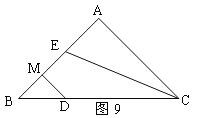
【题目】如图，在等边三角形ABC中，BD是AC边上的中线，延长BC到E，使CE=CD．
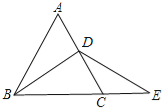
问：
（1）DB与DE相等吗？
（2）把BD是AC边上的中线改成什么条件，还能得到同样的结论？
【答案】（1）相等；（2）BD是
的平分线或BD是AC边上的高．
【解析】试题分析：（1）由CD=CE，得到∠E=∠EDC，由于∠ACB=60°，求得∠E=30°，于是得到∠E=∠DBC，根据等腰三角形的判定即可得到结论；
（2）根据等边三角形“三线合一”的性质，即可得到结论．
解：（1）相等，
理由：∵CD=CE，
∴∠E=∠EDC，
又∵∠ACB=60°，
∴∠E=30°，
又∵∠DBC=30°，
∴∠E=∠DBC，
∴DB=DE；
（2）把BD是AC边上的中线改为BD是∠ABC的平分线或BD是AC边上的高，根据等边三角形“三线合一”的性质，还能得出DB=DE．
名校课堂系列答案【题目】实施新课改以来，某班学生经常采用“小组合作学习”的方式进行学习，学习委员小兵每周对各小组合作学习的情况进行了综合评分．下表是其中一周的统计数据：
组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
分 值 | 90 | 95 | 90 | 88 | 90 | 92 | 85 |
这组数据的中位数和众数分别是
A. 88，90 B. 90，90 C. 88，95 D. 90，95
【题目】 “十
一”黄金周期间，西安大唐芙蓉园在7天假期中每天接待游客的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）。
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 （万人） | +1．6 | +0．8 | +0．4 | -0．4 | -0．8 | +0．2 | -1．4 |
（1）若9月30日的游客人数为
万人，则10月2日的游客人数为_______万人；
（2）七天内游客人数最大的是10月_______日；
（3）若9月30日游客人数为3万人，门票每人120元。请求出黄金周期间西安大唐芙蓉园门票总收入是多少万元？
【题目】某同学在学习了统计知识后，就下表所列的5种用牙不良习惯对全班每一个同学进行了问卷调查（每个被调查的同学必须选择而且只能在5种用牙不良习惯中选择一项），调查结果如下统计图所示．根据以上统计图提供的信息，回答下列问题：
种类 | A | B | C | D | E |
不良习惯 | 睡前吃水果喝牛奶 | 用牙开瓶盖 | 常喝饮料嚼冰 | 常吃生冷零食 | 磨牙 |
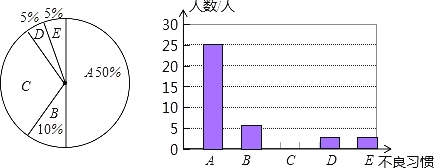
（1）这个班有多少名学生？
（2）这个班中有C类用牙不良习惯的学生多少人？占全班人数的百分比是多少？
（3）请补全条形统计图；
（4）根据调查结果，估计这个年级850名学生中有B类用牙不良习惯的学生多少人？
